New exercises and problems in Mathematics
April
2004
Please read The Conditions of the Problem Solving Competition.
 | New exercisesMaximum score for each exercise (sign "C") is 5 points. |
C. 760. We paid with a 1000-forint (HUF) note in the grocery shop. The bill showed the amount to be payed and the amount we got back. We observed that these two numbers had the same digits but in different orders. What was the sum of the digits?
C. 761. Given the lengths of two sides of a triangle, and given that the corresponding medians are perpendicular, calculate the length of the third side.
C. 762. The surface area of the circumscribed sphere of a cube K1 is twice the surface area of the inscribed sphere of another cube K2. Let V1 denote the volume of the inscribed sphere of the cube K1 and let V2 denote the volume of the circumscribed sphere of the cube K2. Determine the ratio \(\displaystyle \frac{V_1}{V_2}\).
C. 763. There are three 30 cm x40 cm shelves on a stand in the corner of a room. The distances between them are equal. There were three spiders sitting at the point where the middle shelf and both walls meet. One of them crawled diagonally up one wall to the corner of the upper shelf. Another spider crawled diagonally down the other wall to the corner of the lower shelf. The third one remained where it was and observed that he could see his fellows at an angular distance of 120o from each other. Find the (equal) separation between the shelves.
C. 764. Given the real number s, solve the inequality \(\displaystyle \log_{\frac{1}{s}}\log_s\)\log_s \log_sx">.
 | New problemsThe maximum scores for problems (sign "B") depend on the difficulty. It is allowed to send solutions for any number of problems, but your score will be computed from the 6 largest score in each month. |
B. 3722. The secant passing through the intersections of a circle of 4-cm radius centred at O1 and a circle of 6-cm radius centred at O2 intersects the line segment O1O2 at the point T. The length of O1O2 is not smaller than 6 cm. The larger circle intersects the line segment O1O2 at A, the smaller circle intersects it at B, and AT:BT =1:2. Find the length of the line segment O1O2. (3 points) (Suggested by Sz. Békéssy, Budapest)
B. 3723. We have prepared a convex solid out of pentagons and hexagons. Three faces meet at every vertex. Each pentagon is attached to five hexagons along its edges, and each hexagon has common edges with three pentagons. How many faces does the solid have? (4 points)
B. 3724. Find all polynomials p(x) for which the polynomials p(x).p(x+1) and p(x+p(x)) are identically equal. (4 points)
B. 3725. Prove that if a and b are positive numbers then \(\displaystyle 2\sqrt a+3\sqrt[3]{b}\ge5\sqrt[5]{ab}\). (4 points)
B. 3726. What is the digit preceding the decimal point in the number \(\displaystyle \big(3+\sqrt{7}\,\big)^{2004}\)? (4 points)
B. 3727. In a convex quadrilateral, the square of the distance between the midpoints of each pair of opposite sides is equal to one half the sum of the squares of those two sides. Prove that the quadrilateral is a rhombus. (4 points)
B. 3728. Consider the sequence with a0=1 where a2n+1=an and a2n+2=an+an+1 for all integers n\(\displaystyle \ge\)0. Prove that every positive rational number occurs among the elements of the set
\(\displaystyle \left\{\frac{a_{n+1}}{a_n}\colon n\ge1\right\}=\left\{\frac{1}{1},\frac{1}{2}, \frac{2}{1},\frac{1}{3},\frac{3}{2},\dots\right\}. \)
(5 points)
B. 3729. The triangle ABC has unit area. E, F and G are points on the sides BC, CA and AB, respectively, such that AE bisects BF at the point R, BF bisects CG at the point S, and finally CG bisects AE at the point T. Find the area of the triangle RST. (5 points)
B. 3730. The common centre of a circle ka of radius a and a circle kb of radius b (a>b) is O. One of the tangents drawn from a point A lying on ka to the circle kb touches kb at E. The perpendicular drawn to the radius OE at an arbitrary point P of it intersects kb at the points Q and R, and intersects the line AO at the point T. The points S1 and S2 are obtained by marking off those points of the perpendicular drawn to AO at T whose distance from T are equal to PQ. What is the locus of the points Si as P moves along the radius OE? (4 points) (Suggested by M. Kárpáti, Bük)
B. 3731. How many positive integers \(\displaystyle \overline{a_1a_2\dots a_{2n}}\) are there, such that none of the digits are 0 and the sum a1a2+a3a4+...+a2n-1a2n is even? (5 points)
 | New advanced problemsMaximum score for each advanced problem (sign "A") is 5 points. |
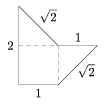
A. 344. Does there exist such a lattice rectangle which can be decomposed into lattice pentagons congruent to the one shown in the Figure?
A. 345. Let r and s be arbitrary positive integers and let t be the minimum of \(\displaystyle 2^k\big(\lceil r/2^k\rceil+\lceil s/2^k\rceil-1\big)\) on the nonnegative integer values of k. Prove that (a) \(\displaystyle \binom{t}{j}\) is even whenever t-s<j<r; (b) t is the smallest integer with this property. (\(\displaystyle \lceil x\rceil\) denotes the smallest integer not smaller than x.)
A. 346. Determine all functions \(\displaystyle f\:\mathbb{Q}\to\mathbb{R}\) satisfying f(xy)=f(x)f(y) and f(x+y)\(\displaystyle \le\)max (f(x),f(y)) for all x, y real numbers.
Send your solutions to the following address:
- KöMaL Szerkesztőség (KöMaL feladatok),
Budapest 112, Pf. 32. 1518, Hungary
