Exercises and problems in Physics
May 2004

Please read The Conditions of the Problem Solving Competition.

Experimental problem

M. 252. Determine the force-dilation characteristics of a rubber band from a hat of a given length. Measure the frequency of the small vertical oscillations under different loads. What connection can be shown between the frequency-load function and the force-dilation characteristics?

(6 points)

Theoretical problems It is allowed to send solutions for any number of problems, but final scores of students of grades 9-12 are computed from the 5 best score in each month. Final scores of students of grades 1-8 are computed from the 3 best scores in each month.

P. 3712. At the 1996 Olympic games Frank Fredericks ran 9.89 seconds in the 100 m race and 19.68 seconds in the 200 m. The same year in an indoor competition he ran the 100 m in 10.05 seconds and 200 m in 19.92 seconds. a) Why is it that the indoor times are worse than those done outdoors? b) Why are the times in the 200 m less than twice the times done on 100 m?

(4 points)

P. 3713. A jeep of a weight of 12 000 N is proceeding up a slope with a velocity of 10 m/s. The height of the slope is 5 m and its length is 30 m. What is the minimum power output of the engine of the jeep?

(3 points)

P. 3714. A good model for calculating the action of the springs of a car is a homogeneous rectangular plate of mass m and of side lengths a and b supported by springs of spring constant D at its four corners. Determine the frequency of the back-and-forth and the left-right sways, if a=3 m, b=1.5 m, m=100 kg, D=50 kN/m.

(4 points)

P. 3715. Water squirts upwards with a 10 m/s initial velocity from a vertical pipe of a cross section of 4 cm². Estimate the force the water jet exerts on a horizontal plate placed 1 m above the end of the pipe.

(4 points)

P. 3716. When an aeroplane takes off or lands in order to decrease the difference between the outside and inside pressure air is removed from or pumped into the passenger cabin. After landing the pressure in the cabin is 95% of the outside pressure. The air temperature is 22 ^oC both inside and outside. We open the pressure-balancing valve for a short while then close it. With the help of a proper model estimate the resulting inside temperature if the heat transfer at the wall of the plane is negligible.

(5 points)

P. 3717. In the circuit shown in the figure R₁=60 \(\displaystyle \Omega\), R₂=30 \(\displaystyle \Omega\) and the internal resistance of the battery of voltage U₀ is negligible. At what R_x value will the power on R_x be the greatest? How much is U₀ if this maximum power is 11.25 W?

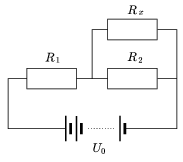
(4 points)

P. 3718. Why does the apparent perpetuum mobile described below not work? Let two charges Q and -Q advance towards each other in air. Exploit the work done by the attractive force, then push them both into an oil tank where the attractive force is lower and using some energy gained previously pull them apart until they reach their initial position and begin the cycle again ... 

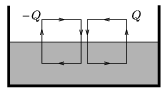
(5 points)

P. 3719. A radar station emits impulses of 10^-6 s duration, one thousand a second at a uniform rate. What is the minimum and maximum range of the radar?

(4 points)

P. 3720. We segregate a parallel beam from the sunshine and let it through an optical grate of a grating constant of 0.01 mm. How wide are the spectra projected on a screen at a distance of 3 m? Can we see here mixed colors (purple for example)?

(4 points)

P. 3721. A particle of a rest mass of m₀ advances at a velocity of v and decays into two photons. a) What is the minimum angle that can be contained by the paths of the two photons? b) If the two photons move in the opposite direction, how much can their energy be (at most)?

(5 points)

Send your solutions to the following address:

KöMaL Szerkesztőség (KöMaL feladatok),
Budapest 112, Pf. 32. 1518, Hungary

solutions@komal.elte.hu.

Deadline: 11 June 2004