New exercises and problems in Mathematics
October 2004

Please read The Rules of the Problem Solving Competition.

New exercises for beginners Solutions can be submitted only by students of grade 9. Maximum score for each exercise (sign "K") is 6 points.

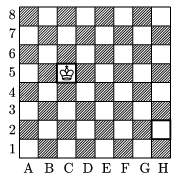
K. 7. In how many different ways can a king move from field C5 to field H2 on a chessboard along some shortest path (i.e. in the minimum number of steps)?

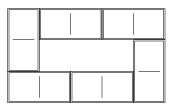
K. 8. The diagram below shows the pattern of rails at a railway station along a single-track railway line. In how many different ways can a train arriving from the left pass through the station?

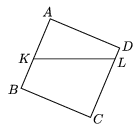
K. 9. A cubic container of edge 12 cm is \(\displaystyle \frac{5}{8}\) full of liquid. It is tilted along an edge. The diagram shows the cross section of the container and the liquid in it. Given that the line segment LC is exactly twice as long as the line segment KB, find the length of LC.

K. 10. Find all perfect squares that contain only odd digits. (Suggested by T. Halász, Budapest)

K. 11. We have arranged a closed chain of six different dominoes on the table, following the rules of the game. The six stones have D dots on them altogether. What is the lowest possible value of D? (A domino stone may have 0 to 6 dots on each side.)

K. 12. For how many positive numbers n is it true that 2004ⁿ is a factor of 2004! ? [2004! denotes the product of integers from 1 to 1024.] (Suggested by Á. Englert, Zalaegerszeg.)

New exercises Maximum score for each exercise (sign "C") is 5 points.

C. 775. My little brother has an ingenious way of counting on his fingers. He starts with 1 on his thumb, continues with 2 and 3 on his index finger, then 4, 5 and 6 on his middle finger, 7 on his ring finger and 8 and 9 on his little finger. Then he continues backwards with 10, 11 and 12 on his ring finger, 13 on his middle finger, 14 and 15 on his index finger, 16, 17 and 18 on his thumb, 19 on his index finger turning back again, and so on. On which finger will he count 2004?

C. 776. Give an example for a right-angled triangle that can be divided into five congruent triangles.

C. 777. At one end of a bus ticket there is a 3 by 3 table of numbered fields 1 to 9 on it. When getting on the bus, the passenger inserts the ticket face up in a slot, and a machine punches some of the fields (it may punch all of them). The machines are not supposed to allow such settings that will punch the same fields if someone inserts the ticket face down. How many different settings are allowed?

C. 778. Let S_m denote the sum of the first m elements of an arithmetic progression. Prove that \(\displaystyle \frac{S_{n+k}}{n+k}=\frac{S_n-S_k}{n-k}\) for all n>k\(\displaystyle \ge\)1.

C. 779. The dimensions of a rectangular block of ham are 12x12x35 cm and it weighs 5 kg. The block is cut in two pieces along a slant cut, in a parallelogram with sides of 15 and 20 cm. How much may the two pieces weigh?

New problems The maximum scores for problems (sign "B") depend on the difficulty. It is allowed to send solutions for any number of problems, but your score will be computed from the 6 largest score in each month.

B. 3752. Show that if the opposite sides of an octagon are parallel and equal in length then the octagon can be divided into parallelograms. (3 points)

B. 3753. Let S_m denote the sum of the first m elements of a sequence (a_m). Prove that if \(\displaystyle \frac{S_{n+k}}{n+k}=\frac{S_n-S_k}{n-k}\) for every positive integer n\(\displaystyle \ne\)k, then (a_m) is an arithmetic progression. (3 points)

B. 3754. Prove that an equilateral triangle cannot be divided into five congruent triangles. (5 points)

B. 3755. A circle intersects each side of a convex quadrilateral in a line segment. The sums of the opposite pairs of arcs inside the quadrilateral are equal. Prove that the quadrilateral is cyclic. (4 points)

B. 3756. Eight-digit numbers are partitioned into two sets. One set contains those that can be expressed as the product of two four-digit numbers, and the other set contains those that cannot. Which set has got more elements? (5 points)

B. 3757. The circles k₁ and k₂ intersect at the points A and B. One of their common tangents touches the circles at the points E₁ and E₂, respectively. Prove that the radius of the circle passing through the points A, E₁, E₂ equals that of the circle through B, E₁, E₂. (4 points)

B. 3758. Let n be a positive even number. The numbers 1,2,...,n² are written in the fields of an nxn table so that the entries in the kth row of the table are (k-1)n + 1, (k-1)n + 2, ..., (k-1)n + n in this order from left to right (k = 1,2,...,n). The fields of the table are then coloured either purple or yellow so that half the fields are purple and the other half are yellow in each row and in each column. (One possible colouring is a chessboard pattern.) Prove that for all such colourings the sums of the numbers in the fields of the same colour are equal. (4 points)

B. 3759. Prove that (2k)! is divisible by k!(k+1)! for every positive integer k. (4 points)

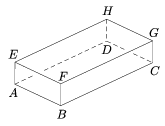
B. 3760. In the cuboid of the figure, S is the midpoint of the edge EH, R is the midpoint of the edge HG and Q is the midpoint of the edge GF. Prove that the triangles ASR and DRQ have equal areas. (4 points)

B. 3761. Solve the following simultaneous equations:

\(\displaystyle \frac{1}{x}+\frac{1}{2y}=(x^2+3y^2)(3x^2+y^2),\)

\(\displaystyle \frac{1}{x}-\frac{1}{2y}=2(y^4-x^4).\)

(5 points)

New advanced problems Maximum score for each advanced problem (sign "A") is 5 points.

A. 353. Prove that the sequences \(\displaystyle {2^{2^n}+1}\) and \(\displaystyle {6^{2^n}+1}\) together contain infinitely many composite numbers.

A. 354. Prove that

\(\displaystyle 2+\frac{1}{1+\cfrac{1}{2+\cfrac{2}{3+\cfrac{3}{4+\cfrac{4}{5+\dots}}}}}=e. \)

A. 355. In space city MO there are 100 space stations. Every pair is connected by a tunnel. In 100 of the tunnels there is two-way traffic and in the rest of them there is one-way traffic. 4 space stations are said to be closely linked if it is possible to reach every one of them from any one of the other 3 along tunnels connecting the 4 stations to each other. Design the city MO so that it contains the maximum number of sets of four closely linked stations. Find the maximum and prove it.

Send your solutions to the following address:

KöMaL Szerkesztőség (KöMaL feladatok),
Budapest 112, Pf. 32. 1518, Hungary

solutions@komal.elte.hu.

Deadline:

10 November 2004 for problems K and

15 November 2004 for problems A, B, C.