 Problem A. 385. (November 2005)
Problem A. 385. (November 2005)
A. 385. Find all sequences a1,a2,... of non-negative numbers, such that the sum is finite and
for all positive integers n.
(5 pont)
Deadline expired on December 15, 2005.
Sketch of solution. We use the fact that the limit of the product (running on all primes) is 0 for

 1 and is positive for
1 and is positive for  >1.
>1.
Consider the first n primes p1,...,pn and sieve out the indices which are thie multilpies. We obtain
If n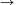
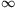 then the left-hand side converges to a1 because all other terms are sieved out.
then the left-hand side converges to a1 because all other terms are sieved out.
If 
 1 then the right-hand side converges to 0, therefore a1=0. Taking a positive integer l and repeating the same procedure for the subsequence akl we obtain al=0.
1 then the right-hand side converges to 0, therefore a1=0. Taking a positive integer l and repeating the same procedure for the subsequence akl we obtain al=0.
If  >1 then the right hand side has a positive limit
>1 then the right hand side has a positive limit . In this case
.
Summarizing the results: for 
 1 the only solution is the constant 0. For
1 the only solution is the constant 0. For  >1, the solution is
>1, the solution is .
Statistics:
9 students sent a solution. 5 points: Erdélyi Márton, Nagy 224 Csaba, Paulin Roland. 4 points: Gyenizse Gergő, Hujter Bálint, Kónya 495 Gábor. 3 points: 1 student. 2 points: 2 students.
Problems in Mathematics of KöMaL, November 2005
