Mathematical and Physical Journal
for High Schools
Issued by the MATFUND Foundation
Already signed up?
New to KöMaL?

Problem A. 432. (September 2007)

A. 432. Find all integer a for which there exists distinct positive integers x and y such that (axy+1) divides (ax2+1)2.

(5 pont)

Deadline expired on October 15, 2007.

Solution. We show that the desired positive integers x,y exist if and only if a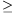\ge-1.

For a=-1, a suitable pair is x=1, y=2 since (ax2+1)2=0.

For a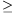\ge0, the pair x=1, y=a+2 is suitable since x<y and (ax2+1)2=axy+1=(a+1)2.

Now consider the case a<-1. Let b=|a|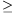\ge2. Call a pair (x,y) of positive integers bad, if x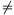\ney and |axy+1|=(bxy-1) divides (ax2+1)2=(bx2-1)2. To the contrary, suppose that there exist at least one bad pair and consider that pair where x is minimal; if there are more than one such pair, then take the smallest possible y for that value of x.

Case 1: x>y. Since

1 \equiv bxy \equiv (bxy)^2 \pmod{bxy-1}

and

(by^2-1)^2 \equiv \big(by^2-(bxy)^2\big)^2 = b^2y^4(bx^2-1)^2 \pmod{bxy-1},

(by2-1)2 is also divisible by (bxy-1). So the pair (y,x) is bad. But y<x which contradicts that we chose the smallest possible x.

Case 2: x<y. Consider the number c=\frac{(bx^2-1)^2}{bxy-1}. Both the numerator and the denominator are positive because b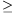\ge2 and x,y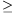\ge1; therefore c is a positive integer. Considering modulo bx,

c \equiv -c(bxy-1) = -(bx^2-1)^2 \equiv -1 \pmod{bx}

hence c=bxz-1 with some positive integer z; then

(bx2-1)2=(bxy-1)(bxz-1).

From x<y we obtain z<x. Then the pair (x,z) is bad. Since z<x<y, this contradicts the choice of y.

Both cases lead to contradiction; bad pairs do not exist for b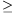\ge2.

Statistics:

11 students sent a solution.
5 points:Korándi Dániel, Lovász László Miklós, Nagy 235 János, Nagy 314 Dániel, Tomon István, Wolosz János.
4 points:Huszár Kristóf.
1 point:1 student.
0 point:2 students.
Unfair, not evaluated:1 solutions.

Problems in Mathematics of KöMaL, September 2007