Problem A. 469. (December 2008)

A. 469. Let 0 $\le$ k $\le$ n and m $\ge$ 2 be integers. Consider the k-element subsets of $\{1,2,\ldots,n\}$ ; in every such subset, compute the residue of the sum of elements, modulo m. Prove that if the m residues are distributed uniformly - i.e. every residue occurs exactly $\frac{\binom{n}{k}}{m}$ times - then n $\ge$ m.

(5 pont)

Deadline expired on February 16, 2009.

Sorry, the solution is available only in Hungarian. Google translation

Megoldásvázlat. Legyen

$S_m(n,k)=\sum_{1\le x_1<x_2<\ldots<x_k\le n} e^{2\pi i \frac{x_1+x_2+\ldots+x_k}m}.$

Az $e^{2\pi i \frac{x_1+x_2+\ldots+x_k}m}$ tag értéke attól függ, hogy $x_1+x_2+\ldots+x_k$ hány maradékot ad m-mel osztva. Ha m>1 és mindegyik maradék ugyanannyiszor, pontosan $\frac{\binom{n}{k}}{m}$ -szer fordul elő, akkor

$S_m(n,k)=\frac{\binom{n}{k}}{m}\sum_{\ell=0}^{m-1}e^{2\pi i\frac{\ell}{m}}=0.$

Az állítás igazolásához tehát elegendő megmutatni, hogy 0 $\le$ k $\le$ n<m esetén S_m(n,k) $\ne$ 0.

Az S_m(n,k) függvényről bebizonyítjuk a következőket:

(a) Ha k=0 vagy k=n, akkor |S_m(n,k)|=1;

(b) Tetszőleges 0<k<n esetén

$S_m(n,k) = S_(n-1,k) + e^{2\pi i\frac{n}{m}} S_n(n-1,k-1);$

(c) Az S_m(n,k) komplex szám párhuzamos (azonos vagy ellentétes irányú) az $e^{\pi i\frac{k(n+1)\pi}m}$ számmal, azaz $\arg S_m(n,k)\equiv\frac{k(n+1)\pi}m~(\mod\pi)$ .

Az (a) tulajdonság triviális, mert az S_m(n,k) egyetlen --- egységnyi hosszúságú --- tagból áll.

A (b) bizonyításához adjuk össze külön azokat a tagokat, amikor x_k=n, illetve azokat, amikor x_k<n:

$S_m(n,k) = \sum_{1\le x_1<x_2<\ldots<x_k\le n-1} e^{2\pi i \frac{x_1+x_2+\ldots+x_k}m} + \sum_{1\le x_1<x_2<\ldots<x_{k-1}\le n-1} e^{2\pi i \frac{x_1+x_2+\ldots+x_{k-1}+n}m} =$

$=\sum_{1\le x_1<x_2<\ldots<x_k\le n-1} e^{2\pi i \frac{x_1+x_2+\ldots+x_k}m} + e^{2\pi i \frac{n}m} \sum_{1\le x_1<x_2<\ldots<x_{k-1}\le n-1} e^{2\pi i \frac{x_1+x_2+\ldots+x_{k-1}}m} =$

$= S_m(n-1,k) + e^{2\pi i \frac{n}m} S_m(n-1,k-1).$

A (c) tulajdonság bizonyításához rendezzük párokba a szám k-asokat; legyen $(x_1,x_2,\ldots,x_k)$ párja (n+1-x_k,n+1-x_k-1,...,n+1-x₁). Tetszőleges k-asra az $e^{2\pi i \frac{x_1+\ldots+x_k}m}$ és $e^{2\pi i \frac{(n+1-x_k)+\ldots+(n+1-x_1)}m}$ komplex számok szimetrikusak $e^{\pi i\frac{k(n+1)\pi}m}$ irányára. Előfordulhat, hogy egy k-as a saját párja, ilyenkor $e^{2\pi i \frac{x_1+\ldots+x_k}m}=1\cdot e^{\pi i\frac{k(n+1)\pi}m}$ .

Az S_m(n,k) összegben szereplő tagokat tehát úgy rendezhetjük párokba és különálló tagokra, hogy ezekben az összeg mind valamilyen valós számszorosa az $e^{\pi i\frac{k(n+1)\pi}m}$ számnak. A (c) tujadonság tehát igaz.

Ezek után n szerinti idukcióval igazoljuk, hogy S_m(n,k) $\ne$ 0, ha n<m. Az n=0 és n=1 esetekben ez következik az (a) tulajdonságból. Tegyük fel tehát, hogy 2 $\le$ n<m és kisebb n-ekre az állítást már igazoltuk. Az (a) miatt elég a 0<k<n esetet vizsgálni.

Tekintsük ismét a (b) összefüggést:

$S_m(n,k) = S_m(n-1,k) + e^{2\pi i\frac{n}{m}} S_m(n-1,k-1);$

Az indukciós feltevés szerint a jobboldalon álló két tag egyike sem 0. Mivel pedig

$\arg S_m(n-1,k) - \arg \left(e^{2\pi i\frac{n}{m}}S_m(n-1,k-1)\right) \equiv \pi\frac{kn}{m} - \pi\frac{(k+1)n}{m} = -\pi\frac{k}{m}$

nem többszöröse $\pi$ -nek, a két tag nem párhuzamos.

A (b) tulajdonság tehát két olyan, 0-tól különböző komplex szám összegeként állítja elő S_m(n,k)-t, amelyek nem párhumazosak.

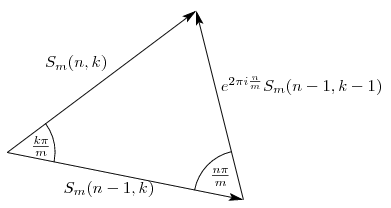
Megjegyzés. Az S_m(n,k), S_m(n-1,k) és $e^{2\pi i\frac{n}{m}}S_m(n-1,k-1)$ komplex számok egy olyan háromszöget alkotnak, amelynek ismerjük a szögeit. Ha a háromszögre felírjuk a szinusztételt, kiszámíthatjuk az oldalak hosszát is; például

$\frac{\big|S_m(n,k)\big|}{\big|S_m(n-1,k-1)\big|} = \frac{\sin\frac{n\pi}m}{\sin\frac{k\pi}m}.$

Ezek után könnyen kiszámítható S_m(n,k) hossza.

A fenti módszerrel belátható, hogy

(*)	$S_m(n,k) = \frac{\sin\frac{n\pi}m\cdot \sin\frac{(n-1)\pi}m\cdot\ldots\cdot \sin\frac{(n-k+1)\pi}m}{ \sin\frac{k\pi}m\cdot \sin\frac{(k-1)\pi}m\cdot\ldots\cdot \sin\frac{\pi}m} e^{\pi i\frac{k(n+1)\pi}m}.$

Természetesen a (*) képletet közvetlenül a (b) tulajdonságból is igazolhatjuk indukcióval --- legalábbis ha a képletet előtte egy kismadár megsúgja nekünk.

Statistics:

3 students sent a solution.

5 points: Nagy 235 János, Tomon István.

1 point: 1 student.

Problems in Mathematics of KöMaL, December 2008

3 students sent a solution.
5 points:	Nagy 235 János, Tomon István.
1 point:	1 student.

Already signed up?
New to KöMaL?