Problem A. 494. (December 2009)

A. 494. Let p₁,...,p_k be prime numbers, and let S be the set of those integers whose all prime divisors are among p₁,...,p_k. For a finite subset A of the integers let us denote by $\mathcal{G}(A)$ the graph whose vertices are the elements of A, and the edges are those pairs a,b 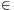$\in$ A for which a-b 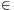$\in$ S. Does there exist for all m 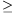$\ge$ 3 an m-element subset A of the integers such that (a) $\mathcal{G}(A)$ is complete? (b) $\mathcal{G}(A)$ is connected, but all vertices have degree at most 2?

Miklós Schweitzer Memorial Competition, 2009

(5 pont)

Deadline expired on January 11, 2010.

Solution. (a) NO.

Let q be the least prime which is not listed among p₁,...,p_k.

If |A|>q then A has two element which are congruent modulo q. Their difference is divisible q, so these elements are not connected.

Therefore, $\mathcal{G}(A)$ cannot be complete if |A|>q.

(b) YES.

Let $a_n=\sum_{i=1}^n (p_1p_2\cdots p_k)^i$ (n=1,2,...). By the definition, a_n+1-a_n=(p₁p₂^...p_k)ⁿ⁺¹ 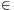$\in$ S.

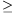We show that $a_N-a_n\not\in S$ for any N $\ge$ n+1. By the definition.

$a_N-a_n = (p_1p_2\cdots p_k)^{n+1} + (p_1p_2\cdots p_k)^{n+2} + \ldots + (p_1p_2\cdots p_k)^N.$

For each i, all terms are divisible by p_iⁿ⁺², except the first one. Hence, the complete sum is not divisible by p_iⁿ⁺²-vel; the greates element of S, which divides a_N-a_n is (p₁p₂^...p_k)ⁿ⁺¹, less than a_N-a_n.

Therefore, for the choice $A=\{a_1,a_2,\ldots,a_m\}$ , the graph $\mathcal{G}(A)$ is a simple path.

Statistics:

11 students sent a solution.

5 points: Backhausz Tibor, Bodor Bertalan, Éles András, Frankl Nóra, Mester Márton, Nagy 235 János, Nagy 648 Donát, Somogyi Ákos, Weisz Ágoston.

2 points: 1 student.

0 point: 1 student.

Problems in Mathematics of KöMaL, December 2009

11 students sent a solution.
5 points:	Backhausz Tibor, Bodor Bertalan, Éles András, Frankl Nóra, Mester Márton, Nagy 235 János, Nagy 648 Donát, Somogyi Ákos, Weisz Ágoston.
2 points:	1 student.
0 point:	1 student.

Already signed up?
New to KöMaL?