Problem A. 569. (October 2012)

A. 569. Call a set $A\subset\mathbb{Z}$ interesting if 2y-x 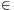$\in$ A for all pairs x,y 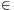$\in$ A with x<y. Let a₁<a₂<...<a_k be positive integers (k 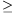$\ge$ 2) whose greatest common divisor is 1. Prove that if A is an interesting set and $\{0,a_1,\ldots,a_k\}\subset A$ then a₁+a_k-3 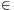$\in$ A.

Proposed by: Carlos Gustavo T. A. Moreira (Gugu), Rio de Janeiro

(5 pont)

Deadline expired on November 12, 2012.

Solution. We prove a more general statement.

Lemma. If a₀<a₁<...<a_k (k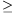 $\ge$ 2) are elements of an interesting set A, the greatest common divisor of (a₁-a₀), (a₂-a₀), ..., (a_k-a₀) is 1, and s=a_k+a₁-a₀-3, then {s,s+1,s+2,...} 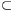$\subset$ A.

In the particular case a₀=0 this implies s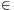 $\in$ A.

We prove the Lemma by induction on (a_k-a₀).

In the case a_k-a₀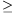 $\ge$ 2 we have k=2, a₁=a₀+1 and a₂=a₀+2, therefore s=a₂+a₁-a₀-3=a₀. So, s=a₀ 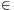$\in$ A, s+1=a₁ 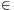$\in$ A, és s+2=a₂ 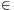$\in$ A. The set A is interesting, for every integer x, x 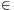$\in$ A and x+1 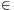$\in$ A impiles x+2=2(x+1)-x 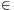$\in$ A. Hence, s,s+1,s+2,... are all elements of A.

Now suppose that a_k-a₀>2, and consider the numbers a₁,a₂,...,a_k and 2a₁-a₀. We will apply the induction hypothesis to these numbers.

Since A is interesting 2a₁-a₀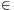 $\in$ A. Among 2a₁-a₀,a₁,a₂,...,a_k the number a₁ is the smallest. The greatest common divisor of (a₂-a₁),...,(a_k-a₁) and (2a₁-a₀)-a₁) also is 1, due to (a_i-a₁,(2a₁-a₀)-a₁)=(a_i-a₁,a₁-a₀)=(a_i-a₀,a₁-a₀).

Case 1: There are at most 2 different values among 2a₁-a₀,a₁,a₂,...,a_k.

Since a₂,...,a_k and 2a₁-a₀ are all greater thatn a₁, this means k=2 and 2a₁-a₀=a₂. Then a₂-a₀=2(a₁-a₀). The numbers a₂-a₀ and a₁-a₀ must be co-primes, so a₁-a₀=1 and a₂-a₀=2; this contradicts the assumption a_k-a₀>2.

Case 2: There are at least 3 distict values among 2a₁-a₀,a₁,a₂,...,a_k, and 2a₁-a₀<a₂.

Apply the induction hypothesis to b₀=a₁<b₁=2a₁-a₀<b₂=a₂<...<b_k=a_k. (This is allowed by b_k-b₀=a_k-a₁<a_k-a₀.) Let t=b_k+b₁-b₀-3. By the hypothesis $\{t,t+1...\}\sbset A$ . Due to t=a_k+(2a₁-a₀)-a₁-3=s, this is what we need.

Case 3: There are at least 3 distict values among 2a₁-a₀,a₁,a₂,...,a_k, and 2a₁-a₀>a_k.

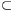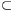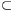Apply the induction hypothesis to b₀=a₁,b₁=a₂,...,b_k-1=a_k,b_k=2a₁-a₀. (Not that b_k-b₀=a₁-a₀<a_k-a₀.) Let t=b_k+b₁-b₀-3. By the hypothesis, {t,t+1...} $\subset$ A. By t=(2a₁-a₀)+a₂-a₁-3=a₂+a₁-a₀-3 $\le$ s, we have {s,s+1,...} $\subset$ {t,t+1,...} $\subset$ A.

Case 4: There are at least 3 distict values among 2a₁-a₀,a₁,a₂,...,a_k, and a₂ $\le$ 2a₁-a₀ $\le$ a_k.

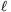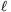Sort the numbers a₁,...,a_k and 2a₁-a₀ in increasing order; let the ordered sequence be $b_0<b_1<...<b_\ell$ , where $\ell$ =k or $\ell$ =k-1, b₀=a₁, b₁=a₂ és $b_\ell=a_k$ .

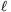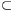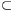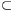Let $t=b_\ell+b_1-b_0-3$ . Due to b $\ell$ -b₀=a_k-a₁<a_k-a₀, we can apply the induction hypothesis to get {t,t+1,...} $\subset$ A. Since t=a_k+a₂-a₁-3 $\le$ a_k+(2a₁-a₀)-a₁-3=s, we have {s,s+1,...} $\subset$ {t,t+1,...} $\subset$ A.

Statistics:

8 students sent a solution.

5 points: Janzer Olivér, Nagy Róbert, Omer Cerrahoglu, Szabó 789 Barnabás.

1 point: 1 student.

0 point: 3 students.

Problems in Mathematics of KöMaL, October 2012

8 students sent a solution.
5 points:	Janzer Olivér, Nagy Róbert, Omer Cerrahoglu, Szabó 789 Barnabás.
1 point:	1 student.
0 point:	3 students.

Already signed up?
New to KöMaL?