 Problem B. 4316. (December 2010)
Problem B. 4316. (December 2010)
B. 4316. Let E denote the point closer to vertex B that divides side BC of a square ABCD in a 1:4 ratio. Let F be the point obtained by reflecting about C the point closer to D that divides side CD in a 1:2 ratio. Prove that the lines AE and BF intersect on the circumscribed circle of the square ABCD.
Suggested by J. Szászné Simon, Budapest
(4 pont)
Deadline expired on January 10, 2011.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Elegendő azt megmutatni, hogy \(\displaystyle CMB\sphericalangle=135^\circ\). Mivel a \(\displaystyle CMB\) szög nagyobb a \(\displaystyle 45^\circ\)-nál nyilván nagyobb \(\displaystyle CFB\) szögnél, ez egyenértékű azzal, hogy \(\displaystyle \sin CMF\sphericalangle=1/\sqrt{2}\). Legyen a négyzet oldala egységnyi, ekkor \(\displaystyle CF=2/3\). A \(\displaystyle CFM\) háromszögben
\(\displaystyle \sin CFM\sphericalangle=\sin CFB\sphericalangle=\frac{CB}{FB}=\frac{1}{\sqrt{CF^2+CB^2}}=\frac{3}{\sqrt{13}}.\)
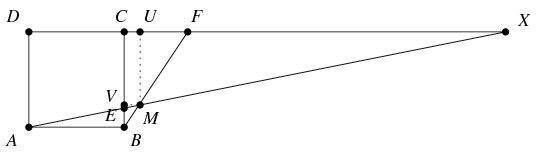
A \(\displaystyle CM\) szakasz hosszának meghatározásához tekintsük az \(\displaystyle AE\) és \(\displaystyle DC\) egyenesek \(\displaystyle X\) metszéspontját. Az \(\displaystyle ABE\) és \(\displaystyle XCE\) háromszögek hasonlóságából \(\displaystyle CX=CX:AB=CE:BE=4\). Ezért \(\displaystyle FX=CX-CF=10/3\), vagyis az \(\displaystyle M\) pont az \(\displaystyle FB\) szakaszt \(\displaystyle FX:AB=10:3\) arányban osztja. Ha az \(\displaystyle M\) pont vetülete a \(\displaystyle CF\) és \(\displaystyle CB\) szakaszokra \(\displaystyle U\), illetve \(\displaystyle V\), akkor ennek alapján \(\displaystyle CV=\frac{10}{13}CB=\frac{10}{13}\) és \(\displaystyle CU=\frac{3}{13}CF=\frac{2}{13}\), ahonnan
\(\displaystyle CM=\sqrt{CU^2+CV^2}=\frac{2\sqrt{2}}{\sqrt{13}}.\)
Végül a szinusz-tétel alapján
\(\displaystyle \sin CMF\sphericalangle=\frac{CF}{CM}\cdot\sin CFM\sphericalangle=1/\sqrt{2},\)
ahogyan azt bizonyítani kívántuk.
Statistics:
116 students sent a solution. 4 points: 96 students. 3 points: 11 students. 2 points: 4 students. 1 point: 1 student. 0 point: 3 students. Unfair, not evaluated: 1 solutions.
Problems in Mathematics of KöMaL, December 2010
