Problem B. 4321. (December 2010)

B. 4321. Prove that the following inequality is true in every triangle: $\frac{b}{\sin \left(\gamma + \dfrac{\alpha}{3}\right)} + \frac{c}{\sin \left(\beta + \dfrac{\alpha}{3}\right)} > \frac{2}{3} \cdot \frac{a}{\sin \left(\dfrac{\alpha}{3}\right)}$ .

From the journal Ifjúsági Matematikai Lapok, Kolozsvár

(5 pont)

Deadline expired on January 10, 2011.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. A háromszög csúcsait a szokásos módon jelölve, az $\displaystyle A$ csúcsból húzott szögharmadolóknak a körülírt körrel alkotott metszéspontjait jelölje $\displaystyle D$ és $\displaystyle E$ az ábrán látható módon.

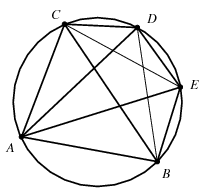
A kerületi szögek tétele szerint $\displaystyle CD=DE=EB=d$, továbbá a $\displaystyle BCE$ és $\displaystyle CBD$ szögek nagysága egyaránt $\displaystyle \alpha/3$. Így a szinusz-tétel alapján a bizonyítandó egyenlőtlenség ekvivalens az

$\displaystyle \frac{AC}{AE}+\frac{AB}{AD}>\frac{2}{3}\cdot\frac{BC}{DE},$

vagyis a

$\displaystyle 3AC\cdot AD\cdot DE+3AB\cdot AE\cdot DE>2BC\cdot AD\cdot AE$

egyenlőtlenséggel. Az $\displaystyle ABDC$ és $\displaystyle ABEC$ húrnégyszögekre a Ptolemaiosz-tételt felírva kapjuk, hogy

$\displaystyle BC\cdot AD\cdot AE=(AB\cdot CD+AC\cdot BD)AE= (AB\cdot CE+AC\cdot BE)AD.$

Ennek alapján a bizonyítandó egyenlőtlenséget átírhatjuk

$\displaystyle 3AC\cdot AD+3AB\cdot AE> AB\cdot AE +AC\cdot\frac{BD}{d}\cdot AE+AB\cdot\frac{CE}{d}\cdot AD+ AC\cdot AD$

alakra. Minthogy $\displaystyle BD=CE<2d$, elegendő a

$\displaystyle 2AC\cdot AD+2AB\cdot AE\ge 2AC\cdot AE+2AB\cdot AD,$

vagy egyszerűbb alakban, az

$\displaystyle (AC-AB)(AD-AE)\ge 0$

egyenlőtlenséget igazolni, ami a szinusz-tétel alapján ekvivalens a

$\displaystyle (\sin\beta-\sin\gamma)\Bigl(\sin \left(\beta+\frac{\alpha}{3}\right) - \sin \left(\gamma+\frac{\alpha}{3}\right)\Bigr)\ge 0$

egyenlőtlenséggel.

Szimmetria okok miatt feltehetjük, hogy $\displaystyle \beta\ge \gamma$, ekkor $\displaystyle \sin\beta\ge \sin\gamma$. Belátjuk, hogy ekkor a fenti szorzat második tényezője sem negatív. Mivel most $\displaystyle \gamma+\frac{\alpha}{3} <\frac{\pi}{2}$, ez egyet jelent a

$\displaystyle \gamma+\frac{\alpha}{3}\le \beta+\frac{\alpha}{3}\le\pi- \left(\gamma+\frac{\alpha}{3}\right)$

egyenlőtlenséggel, ami viszont nyilvánvalóan teljesül.

A megoldásból az is leolvasható, hogy az egyenlőtlenségben szereplő $\displaystyle \frac{2}{3}$ szorzótényező nem helyettesíthető nagyobb konstanssal; ehhez elegendő azokat a háromszögeket megnézni, amelyekben $\displaystyle \alpha=2\varepsilon$, $\displaystyle \beta=\gamma=\frac{\pi}{2}- \varepsilon$, ahol $\displaystyle \varepsilon$ elegendően kicsi.

Statistics:

17 students sent a solution.

5 points: Bogár Blanka, Damásdi Gábor, Dudás 002 Zsolt, Énekes Péter, Fonyó Viktória, Lenger Dániel, Máthé László, Szabó 928 Attila, Tekeli Tamás, Viharos Andor.

4 points: Perjési Gábor.

3 points: 6 students.

Problems in Mathematics of KöMaL, December 2010

17 students sent a solution.
5 points:	Bogár Blanka, Damásdi Gábor, Dudás 002 Zsolt, Énekes Péter, Fonyó Viktória, Lenger Dániel, Máthé László, Szabó 928 Attila, Tekeli Tamás, Viharos Andor.
4 points:	Perjési Gábor.
3 points:	6 students.

Already signed up?
New to KöMaL?