Problem B. 4468. (September 2012)

B. 4468. Consider two circular discs that have no common points. The circle drawn on the line segment connecting their centres as diameter intersects each of the common exterior tangents at two points. Prove that the diagonals of the quadrilateral formed by the four points of intersection are the common interior tangents.

Suggested by V. Gedeon, Budapest

(5 pont)

Deadline expired on October 10, 2012.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. A körök közös belső érintői a külső érintőket két-két pontban metszik. A bizonyítandó állítást úgy is fogalmazhatjuk, hogy ezen négy pont mindegyike a körök középpontjait összekötő szakasz, mint átmérő fölé rajzolt körvonalra esik. Szimmetria okok miatt ezt elég az egyik metszéspontra igazolni, melyet jelöljön M.

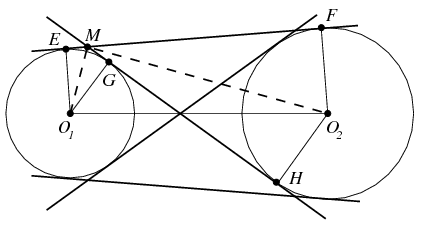
Az ábra jelöléseivel legyen $GO_1O_2\sph=HO_2O_1\sph=\alpha$ , $FO_2O_1\sph=180^\circ-EO_1O_2\sph=\beta$ . Ha a két kör ugyanakkora, akkor $\beta$ derékszög, ha a jobb oldali kör a kisebb, akkor $\beta$ tompaszög, mindenesetre $\alpha$ < $\beta$ <180^o- $\alpha$ . Minthogy az O₂M egyenes felezi az FO₂H szöget, O₁M pedig az EO₁G szöget,

$O_1O_2M\sph=\frac{\alpha+\beta}{2}-\alpha, \qquad O_2O_1M\sph=\alpha+\frac{(180^\circ-\beta)-\alpha}{2}.$

A két szög összege 90^o, vagyis az O₁O₂M háromszög M-nél lévő szöge derékszög. Ez pedig Thalész tétele szerint pontosan azt jelenti, hogy M az O₁O₂ átmérőjű körvonalra esik.

Statistics:

83 students sent a solution.

5 points: 58 students.

4 points: 13 students.

3 points: 3 students.

2 points: 2 students.

1 point: 2 students.

0 point: 5 students.

Problems in Mathematics of KöMaL, September 2012

83 students sent a solution.
5 points:	58 students.
4 points:	13 students.
3 points:	3 students.
2 points:	2 students.
1 point:	2 students.
0 point:	5 students.

Already signed up?
New to KöMaL?