 Problem B. 4477. (October 2012)
Problem B. 4477. (October 2012)
B. 4477. In an acute triangle ABC,  <
< (with conventional notations). Let R and P be the feet of the altitudes drawn from vertices A and C, respectively. Let Q denote a point of line AB, different from P, such that AP.BQ=AQ.BP. Prove that line RB bisects the angle PRQ.
(with conventional notations). Let R and P be the feet of the altitudes drawn from vertices A and C, respectively. Let Q denote a point of line AB, different from P, such that AP.BQ=AQ.BP. Prove that line RB bisects the angle PRQ.
Suggested by J. Mészáros, Jóka
(5 pont)
Deadline expired on November 12, 2012.
Sorry, the solution is available only in Hungarian. Google translation
Útmutatás: Apolloniusz-kör.
Megoldás: Jegyezzük meg, hogy a feladatban megfogalmazott feltétel a Q pontot egyértelműen meghatározza. Azon X pontok mértani helye ugyanis, melyekre AX:BX=AP:BP teljesül, egy olyan Apollóniusz-kör, melynek AB egyenessel vett egyik metszéspontja P. A Q pont tehát a másik metszéspont.
Az APRC négyszög húrnégyszög, ezért , vagyis
. Legyen B' a B pont tükörképe P-re; ez az AP szakasz egy belső pontja. CB'=CB, AB'=AP-BP, az AB'C háromszög szögei pedig rendre
 , 180o-
, 180o- és
és  -
- . Vegyük fel az AB szakasz B-n túli meghosszabbításán azt a Q' pontot, amelyre
. Vegyük fel az AB szakasz B-n túli meghosszabbításán azt a Q' pontot, amelyre . Belátjuk, hogy erre a Q' pontra teljesül AQ':BQ'=AP:BP. Ez azt jelenti, hogy Q'=Q, amiből a feladat állítása azonnal következik, hiszen a Q' pontot úgy vettük fel az AB egyenesen, hogy RB felezze a PRQ' szöget.
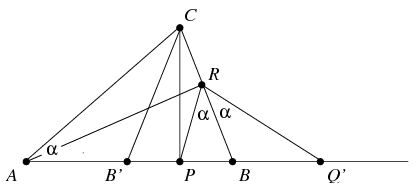
Az RBQ' háromszög szögei is  , 180o-
, 180o- ,
,  -
- . A két háromszög hasonlósága miatt BQ':RB=CB':AB'=CB:AB'. Ennélfogva
. A két háromszög hasonlósága miatt BQ':RB=CB':AB'=CB:AB'. Ennélfogva
Az ABR és CBP háromszögek hasonlósága alapján RB:AB=PB:CB. Így valóban
Statistics:
63 students sent a solution. 5 points: Ágoston Péter, Bingler Arnold, Bogár Blanka, Bősze Zsuzsanna, Dinev Georgi, Fehér Zsombor, Fekete Panna, Fonyó Viktória, Forrás Bence, Gyulai-Nagy Szuzina, Holczer András, Homonnay Bálint, Janzer Barnabás, Janzer Olivér, Kabos Eszter, Kátay Tamás, Kecskés Boglárka, Kúsz Ágnes, Lelkes János, Maga Balázs, Nagy-György Pál, Papp Roland, Petrényi Márk, Sagmeister Ádám, Schultz Vera Magdolna, Schwarcz Tamás, Szabó 789 Barnabás, Szabó 928 Attila, Szász Dániel Soma, Szilágyi Krisztina, Szőke Tamás, Tardos Jakab, Tossenberger Tamás, Tóth László Gábor, Tulassay Zsolt, Varga 149 Imre Károly, Venczel Tünde, Williams Kada. 4 points: Balogh Tamás, Medek Ákos, Mócsy Miklós, Nagy Róbert, Nagy-György Zoltán, Qian Lívia, Sárosdi Zsombor, Seress Dániel, Sticza Gergő, Szabó 262 Lóránt, Weisz Ambrus. 3 points: 3 students. 2 points: 1 student. 1 point: 1 student. 0 point: 4 students. Unfair, not evaluated: 5 solutionss.
Problems in Mathematics of KöMaL, October 2012
