 Problem B. 4583. (December 2013)
Problem B. 4583. (December 2013)
B. 4583. The points D and E lie on the line segment AB. In the same half plane, a regular triangle is drawn over each of the line segments AD, DB, AE and EB. The third vertices are F, G, H and I, respectively. Prove that if the lines FI and GH are not parallel, then their intersection lies on the line AB.
Suggested by Sz. Miklós, Herceghalom
(3 pont)
Deadline expired on January 10, 2014.
Sorry, the solution is available only in Hungarian. Google translation
1. megoldás (vázlat). Ha fecseréljük a D,F,G pontok szerepét az E,I,H pontokkal, az állítás önmagába megy át. Ezért az általánosság sérülése nélkül feltehetjük, hogy AD<AE. Legyen a=AD, b=DE, c=EB.
Ha a=c, akkor az FI és a GH egyenes is párhuzamos AB-vel, és kész vagyunk. A továbbiakban feltételezzük, hogy a c. Legyen M=AB
c. Legyen M=AB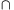 GH és M'=AB
GH és M'=AB FI. Azt akarjuk igazlni, hogy M=M'. Ismét az állítás szimmetriája miatt (
FI. Azt akarjuk igazlni, hogy M=M'. Ismét az állítás szimmetriája miatt (,
,
,
,
) feltehetjük, hogy a<c; ekkor M és M' is a BA félegyenes A-n túli meghosszabbításán van, és a megoldáshoz elég azt ellenőrizni, hogy AM=AM'. Legyen x=AM és x'=AM'.
A párhuzamos szelőt tételét alkalmazzuk az MAB és az MHG egyeneseket párhuzamosan metsző AH és EI, illetve EH és BG szelőire:
x(x+a+b+c)=(x+a+b)(x+a)
Hasonlóan, az M'AB és M'FI egyenesekre felírva a párhuzamos szelők tételét,
x'(x'+a+b+c)=(x'+a)(x'+a+b)
Tehát x'=x és így M=M'; az GH és FI egyenesek az AB egyenes M pontjában metszik egymást.
2. megoldás (vázlat). Írjuk fel a Menelaosz-tételt az ABC háromszögre kétféleképpen, a GHM és az FIM' egyenesre is, Az előző megoldás jeöléseivel
illetve
Láthatjuk, hogy , amiből következi, hogy M'=M.
3. megoldás (vázlat). A megoldáshoz projektív geometriai eszközöket, pontnégyesek kettősviszonyának jól ismert tulajdonságait használjuk fel.
Legyen C=AF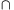 BI. A párhuzamos vetítések és az (XYUV)=(YXVU) azonosság miatt
BI. A párhuzamos vetítések és az (XYUV)=(YXVU) azonosság miatt
(ACFH)=(ABDE)=(CBGI)=(BCIG).
Az (A,C,F,G) és a (B,C,I,G) pontnégyeseknek vagy közös pontja (a C pont), ezért a két pontnégyes perspektív: az AB, FI és HG egyenes (a projektív síkon) egy ponton megy át.
Statistics:
131 students sent a solution. 3 points: 114 students. 2 points: 3 students. 1 point: 7 students. 0 point: 6 students. Unfair, not evaluated: 1 solutions.
Problems in Mathematics of KöMaL, December 2013
