Problem B. 4635. (May 2014)

B. 4635. In an acute-angled triangle \(\displaystyle ABC\), \(\displaystyle AB<AC\). The centre of the circumscribed circle is \(\displaystyle O\), the orthocentre is \(\displaystyle M\). Construct the point \(\displaystyle P\) on the side \(\displaystyle BC\) for which \(\displaystyle AOP\sphericalangle = PMA\sphericalangle\).

(4 pont)

Deadline expired on June 10, 2014.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Legyen \(\displaystyle P\) a kívánt tulajdonságú pont a \(\displaystyle BC\) szakaszon. Ekkor \(\displaystyle AOP\sphericalangle =PMA\sphericalangle\), amit jelöljünk \(\displaystyle \beta\)-val.

Tükrözzük az \(\displaystyle M\) pontot a \(\displaystyle BC\) oldalra, tükörképe legyen \(\displaystyle M'\), ami rajta van a háromszög köré írt körön. A tükrözés miatt \(\displaystyle PMM'\sphericalangle =PM'M\sphericalangle\), melyet jelöljön \(\displaystyle \alpha\).

Mivel \(\displaystyle AMP\sphericalangle +PMM'\sphericalangle =\beta +\alpha =180^{\circ}\), az \(\displaystyle AOPM'\) négyszög húrnégyszög, hiszen két szemközti szögének összege: \(\displaystyle AOP\sphericalangle +PM'M\sphericalangle =\beta +\alpha =180^{\circ}\).

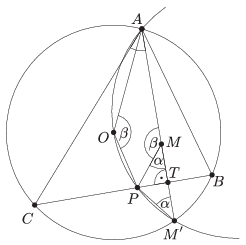
Ezek alapján a \(\displaystyle P\) pont szerkesztése: Az \(\displaystyle M\) magasságpontot tükrözzük a \(\displaystyle BC\) oldalra, majd megszerkesztjük az \(\displaystyle AOM'\) háromszög körülírt körét, ez a kör a \(\displaystyle BC\) oldalt a \(\displaystyle P\) pontban metszi. Mivel \(\displaystyle AB<AC\), az \(\displaystyle AOM'\) háromszög sosem lesz elfajuló, és mindig csak egy megoldás van, mivel a két körülírt kör \(\displaystyle A\)-ban és \(\displaystyle M'\)-ben metszi egymást, így az \(\displaystyle ABC\) háromszög körülírt körén belül csak egy metszéspontja lehet az \(\displaystyle AOM'\) háromszög köré írt körnek és a \(\displaystyle BC\) oldalnak.

Csitári Nóra (Budapesti Fazekas M. Ált. Isk. és Gimn., 9. évf.) dolgozata alapján

Statistics:

14 students sent a solution.
4 points:	Csitári Nóra, Fonyó Viktória, Glattfelder Hanna, Kuchár Zsolt, Nagy-György Pál, Németh Hanna, Sal Kristóf, Szakács Lili Kata, Williams Kada.
2 points:	2 students.
1 point:	2 students.
0 point:	1 student.

Problems in Mathematics of KöMaL, May 2014