Problem B. 4639. (May 2014)

B. 4639. Let \(\displaystyle P\) be an exterior point of the ellipse \(\displaystyle \mathcal E\) with foci \(\displaystyle F_1\) and \(\displaystyle F_2\). It does not lie on the line of the major axis. Let \(\displaystyle M_1\) be the intersection of the line segment \(\displaystyle PF_1\) with \(\displaystyle \mathcal E\), let \(\displaystyle M_2\) be the intersection of the line segment \(\displaystyle PF_2\) with \(\displaystyle \mathcal E\), and let \(\displaystyle R\) be the intersection of the lines \(\displaystyle M_1F_2\) and \(\displaystyle M_2F_1\). Prove that the quadrilateral \(\displaystyle PM_1RM_2\) has an inscribed circle.

Suggested by G. Holló, Budapest

(5 pont)

Deadline expired on June 10, 2014.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Ha \(\displaystyle PM_1RM_2\) érintőnégyszög, akkor a beírható köre egyúttal az \(\displaystyle F_1M_2P\) háromszögnek és az \(\displaystyle F_2M_1P\) háromszögnek is beírható köre. Vizsgáljik meg, hogy e két háromszögben a beírható kör a \(\displaystyle P\) csúcstól milyen távolságra érinti a \(\displaystyle P\)-n átmenő oldalakat. Ha e két távolság egyenlő, akkor a két kör egybeesik, mert az \(\displaystyle F_1PF_2\) szög szárait a szög csúcsától adott távolságra érintő kör egyértelműen létezik, középpontja a szög száraira az adott távolságban állított merőlegesek metszéspontja, sugara pedig e metszéspontnak a száraktól való távolsága (1. ábra).

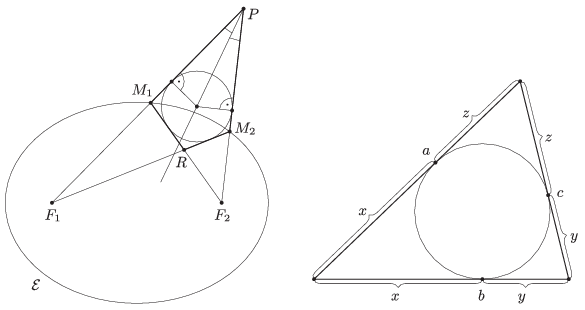
1. ábra                                                             2. ábra

Ismert, hogy ha egy háromszög oldalai \(\displaystyle a,b\) és \(\displaystyle c\), akkkor a beírt kör oldalakon lévő érintési pontjainak a csúcsoktól való távolsága rendre \(\displaystyle (a+b-c)/2\), \(\displaystyle (b+c-a)/2\) és \(\displaystyle (c+a-b)/2\). (Ennek bizonyítását a 2. ábra alapján az olvasóra bízzuk, csak annyit kell felhasználni, hogy külső pontból egy körhöz húzott két érintő hossza megegyezik.)

Az \(\displaystyle F_1M_2P\) háromszög beírt köre tehát \(\displaystyle P\)-től \(\displaystyle \frac{PF_1+PM_2-F_1M_2}2\), az \(\displaystyle F_2M_1P\) háromszög beírt köre pedig \(\displaystyle P\)-től \(\displaystyle \frac{PF_2+PM_1-F_2M_1}2\) távolságra érinti az \(\displaystyle F_1PF_2\) szög szárait. Megmutatjuk, hogy e két távolság egyenlő. Ehhez elegendő azt belátnunk, hogy

\(\displaystyle PF_1+PM_2-F_1M_2=PF_2+PM_1-F_2M_1, \)

azaz

\(\displaystyle (PM_1+M_1F_1)+PM_2-F_1M_2=(PM_2+M_2F_2)+PM_1-F_2M_1 \)

teljesül. Ezt rendezve kapjuk, hogy elegendő megmutatnunk az

\(\displaystyle M_1F_1+F_2M_1=M_2F_2+F_1M_2 \)

egyenlőség fennállását, ami viszont azonnal következik abból, hogy \(\displaystyle M_1\) és \(\displaystyle M_2\) rajta vannak az \(\displaystyle F_1\) és \(\displaystyle F_2\) fókuszú \(\displaystyle {\mathcal E}\) ellipszisen.

Tehát az \(\displaystyle F_1M_2P\) és az \(\displaystyle F_2M_1P\) háromszögek beírható körei egybeesnek, így ez a kör érinti a \(\displaystyle PM_1RM_2\) négyszög minden oldalát, ezért \(\displaystyle PM_1RM_2\) érintőnégyszög.

Fekete Panna (Pécs, Leőwey K. Gimn., 11. évf.) dolgozata alapján

Statistics:

17 students sent a solution.
5 points:	Ágoston Péter, Baran Zsuzsanna, Cseh Kristóf, Fekete Panna, Forrás Bence, Geng Máté, Győrfi-Bátori András, Gyulai-Nagy Szuzina, Kúsz Ágnes, Lajkó Kálmán, Nagy-György Pál, Schrettner Bálint, Simkó Irén, Williams Kada.
4 points:	Török Tímea.
3 points:	1 student.
2 points:	1 student.

Problems in Mathematics of KöMaL, May 2014