Problem B. 4807. (September 2016)

B. 4807. A square is drawn over each side of a right-angled triangle \(\displaystyle ABC\) of unit area, on the outside. Denote the centres of the squares by \(\displaystyle D\), \(\displaystyle E\) and \(\displaystyle F\). Prove that the area of triangle \(\displaystyle DEF\) is at least two.

(Kvant)

(4 pont)

Deadline expired on October 10, 2016.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Használjuk az ábra jelöléseit. Legyenek \(\displaystyle A_1\), \(\displaystyle B_1\), \(\displaystyle C_1\) rendre a \(\displaystyle BC\), \(\displaystyle AC\), \(\displaystyle AB\) oldalak felezőpontjai. A háromszög két befogójának hossza: \(\displaystyle BC=a\), \(\displaystyle AC=b\).

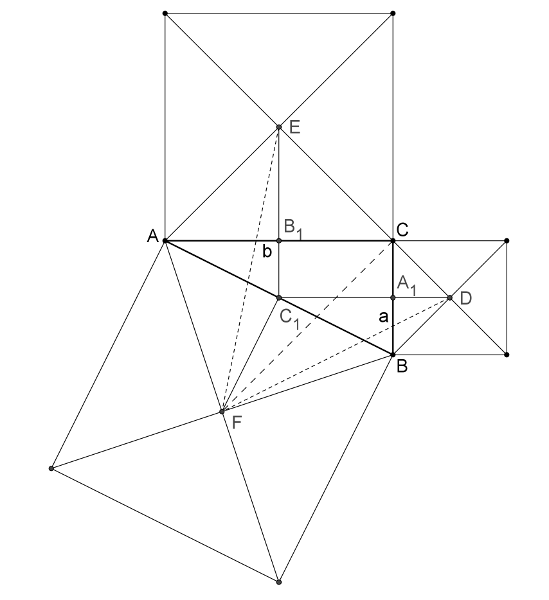
\(\displaystyle B_1C_1=CA_1=\frac a2\), \(\displaystyle A_1C_1=CB_1=\frac b2\), mert középvonalak, \(\displaystyle ACB\angle\) derékszög, ezért a \(\displaystyle CA_1C_1B_1\) négyszög téglalap.

\(\displaystyle B_1EC\) és \(\displaystyle A_1CD\) egyenlő szárú derékszögű háromszögek, így \(\displaystyle B_1E=B_1C=\frac b2\) és \(\displaystyle A_1D=A_1C=\frac a2\). Ekkor \(\displaystyle C_1 E=C_1 B_1+B_1 E=\frac{a+b}{2}=A_1 D+A_1 C_1=C_1 D\). Tehát \(\displaystyle C_1 ED\) is egyenlő szárú derékszögű háromszög, átfogója: \(\displaystyle DE=\sqrt2\cdot C_1 E=\sqrt2\cdot\frac{a+b}{2}=\frac{a+b}{\sqrt2}\).

\(\displaystyle \frac{AC}{AE}=\frac{AF}{AC_1} =\sqrt2\) és \(\displaystyle CAF\angle=CAB\angle+45^{\circ}=EAC_1\angle\). Ezért a \(\displaystyle CAF\) és az \(\displaystyle EAC_1\) háromszögben két oldal aránya és az általuk bezárt szög megegyezik, ezért hasonlóak és a hasonlóság aránya \(\displaystyle \sqrt2\). Így \(\displaystyle CF=\sqrt2\cdot C_1 E=\frac{a+b}{\sqrt 2}\). A hasonlóságból az is következik, hogy a \(\displaystyle CF\) és \(\displaystyle EC_1\) szakaszok egyenese által bezárt szög megegyezik az \(\displaystyle AC\) és \(\displaystyle AE\) szakaszok egyenese által bezárt szöggel, ami \(\displaystyle 45^{\circ}\). Mivel \(\displaystyle C_1 ED=45^{\circ}\), ezért ezekből \(\displaystyle CF\perp DE\) következik. Tehát \(\displaystyle CF\) a \(\displaystyle DEF\) háromszög magassága, így \(\displaystyle T_{DEF}=\frac12\cdot DE\cdot CF=\frac12\cdot \frac{a+b}{\sqrt2}\cdot \frac{a+b}{\sqrt2}=\frac{(a+b)^2}{4}\geq ab=2\cdot T_{ABC}\).

Statistics:

169 students sent a solution.
4 points:	122 students.
3 points:	21 students.
2 points:	10 students.
1 point:	7 students.
0 point:	9 students.

Problems in Mathematics of KöMaL, September 2016