Problem B. 4823. (November 2016)

B. 4823. In an acute-angled triangle \(\displaystyle ABC\) (\(\displaystyle AB < AC\)), the foot of the altitude from vertex \(\displaystyle A\) is \(\displaystyle D\), and the centre of the circumscribed circle is \(\displaystyle O\). Prove that if the exterior angle bisector of \(\displaystyle BAC\sphericalangle\) is parallel to \(\displaystyle OD\), then the diagonals of the quadrilateral \(\displaystyle AODC\) are equal.

Hungarian Mathematics Competition of Transsylvania

(3 pont)

Deadline expired on December 12, 2016.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Azt kell igazolnunk, hogy \(\displaystyle AD=OC\).

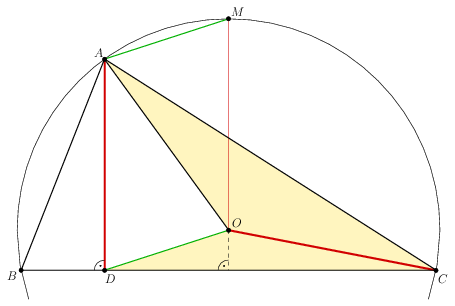
Legyen \(\displaystyle M\) a \(\displaystyle BAC\) körív felezőpontja; jól ismert, hogy a \(\displaystyle BAC\) szög külső szögfelezője átmegy az \(\displaystyle M\) ponton. (Például a kerületi szögek tételéből \(\displaystyle MAC\sphericalangle = MBC\sphericalangle = 90^\circ- BMO\angle = 90^\circ-\frac12 BMC\angle = 90^\circ-\frac12 BAC\angle = 90^\circ-\frac12 \alpha = \frac{180^\circ-\alpha}2\).)

Az \(\displaystyle OM\) és \(\displaystyle OC\) szakaszok a körülírt kör sugarai, így \(\displaystyle OM=OC\).

Az \(\displaystyle M\) és az \(\displaystyle O\) pont is egyenlő távol van a \(\displaystyle B\) és \(\displaystyle C\) pontoktól, így az \(\displaystyle MO\) egyenes a \(\displaystyle BC\) szakasz felező merőlegese. Ezért \(\displaystyle MO\) merőleges a háromszög \(\displaystyle BC\) oldalára, tehát párhuzamos az \(\displaystyle AD\) magassággal. A feladat feltétele szerint az \(\displaystyle AM\) külső szögfelező és \(\displaystyle DO\) is párhuzamosak. Az \(\displaystyle ADOM\) négyszögben tehát a szemközti oldalak párhuzamosak, a négyszög egy paralelogramma. A paralelogramma szemközti oldalai egyenlők, ezért \(\displaystyle AD=OM\).

Összefoglalva, \(\displaystyle AD = OM = OC\).

Statistics:

106 students sent a solution.
3 points:	64 students.
2 points:	33 students.
1 point:	8 students.
0 point:	1 student.

Problems in Mathematics of KöMaL, November 2016