Problem C. 1089. (September 2011)

C. 1089. The area of a quadrilateral ABCD is 20. The vertices are labelled in counterclockwise order. The coordinates of three vertices are A(-2;0), B(2;0) and C(2;4). What is the minimum possible perimeter of the quadrilateral ABCD?

(5 pont)

Deadline expired on October 10, 2011.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Mivel a négyszög pozitív körüljárási irányú, ezért a \(\displaystyle D\) csúcs a \(\displaystyle BA\) és a \(\displaystyle BC\) félegyenesek által meghatározott síknegyed és az \(\displaystyle AC\) egyenes által meghatározott, \(\displaystyle B\)-t nem tartalmazó félsík metszetének belső pontja.

Ekkor az \(\displaystyle ABCD\) négyszög felbontható az \(\displaystyle ABC\) és az \(\displaystyle ACD\) háromszögekre, ezért \(\displaystyle t_{ABCD}=t_{ABC}+t_{ACD}\).

Az \(\displaystyle ABCD\) négyszög területe 20. Az \(\displaystyle ABC\) háromszög területe 8, mivel \(\displaystyle AB\) és \(\displaystyle BC\) derékszöget zárnak be egymással: \(\displaystyle t_{ABC}=\frac{AB\cdot BC}{2}=\frac{4\cdot 4}{2}=8\).

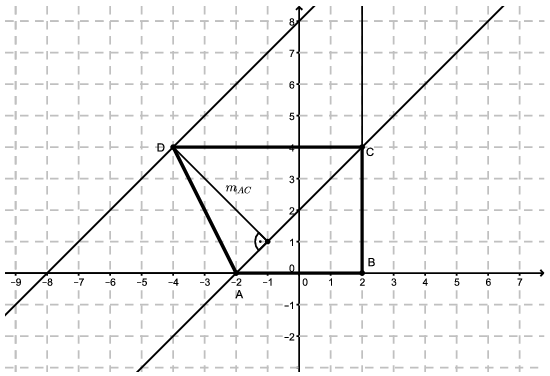
1. ábra

Tehát az \(\displaystyle ACD\) háromszög területe 20-8=12. Az \(\displaystyle AC\) szakasz hossza az \(\displaystyle ABC\) derékszögű háromszögre felírt Pitagorasz-tétel alapján: \(\displaystyle AC=\sqrt{AB^2+BC^2}=\sqrt{2\cdot 16}=4\sqrt{2}\).

Tehát az \(\displaystyle ACD\) háromszög \(\displaystyle AC\) oldala \(\displaystyle 4\sqrt{2}\), területe 12, innen az \(\displaystyle AC\) oldalhoz tartozó \(\displaystyle m_{AC}\) magassága:

\(\displaystyle m_{AC}=\frac{2T_{ACD}}{AC}=\frac{2\cdot12}{4\sqrt2}=\frac{6}{\sqrt{2}}=3\sqrt{2}.\)

Mivel \(\displaystyle m_{AC}\) a \(\displaystyle D\) pont távolsága az \(\displaystyle AC\) szakasztól, ezért a \(\displaystyle D\) pont illeszkedik az \(\displaystyle AC\)-vel párhuzamos, attól \(\displaystyle 3\sqrt{2}\) távolságra lévő \(\displaystyle e\) egyenesre.

Az \(\displaystyle ABCD\) négyszög kerülete a négy oldalának az összege, ebből az \(\displaystyle AB\) és a \(\displaystyle BC\) szakaszok hossza állandó. Tehát a kerület pontosan akkor minimális, amikor az \(\displaystyle AD\) és a \(\displaystyle CD\) szakaszok összege is az.

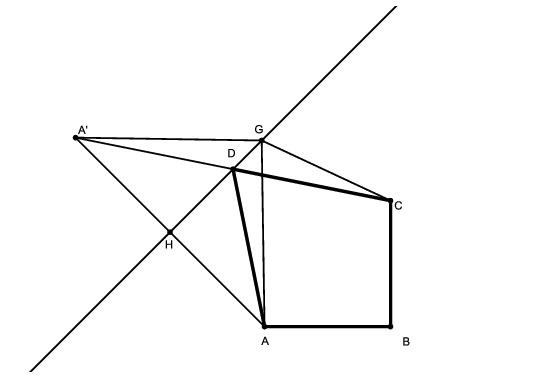
2. ábra

Tekintsünk egy tetszőleges \(\displaystyle G\) pontot az \(\displaystyle e\) egyenesen, és tekintsük azt a \(\displaystyle D\) pontot is, amely az \(\displaystyle A\) pont \(\displaystyle e\)-re vonatkozó \(\displaystyle A'\) tükörképét \(\displaystyle C\)-vel összekötő szakasznak és \(\displaystyle e\)-nek a metszépontja. A tükrözés miatt \(\displaystyle AD=A'D\). Az \(\displaystyle A'GC\) háromszögben a háromszög-egyenlőtlenség miatt \(\displaystyle A'G+GC>A'C=A'D+DC=AD+DC\). Tehát a kerület erre a \(\displaystyle D\) pontra lesz minimális.

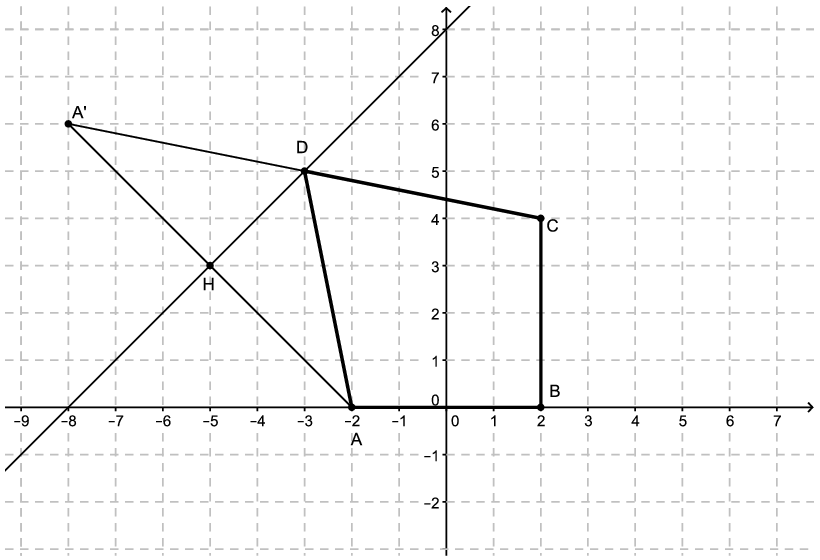
Mivel az \(\displaystyle AC\) egyenes meredeksége 1, ezért a vele párhuzamos \(\displaystyle e\) egyenest könnyen megkapjuk, ha pl. azt a \(\displaystyle H\) pontot tekintjük, amely az \(\displaystyle A\) ponttól \(\displaystyle 3\sqrt2\) távolságra van az \(\displaystyle A\)-n átmenő, \(\displaystyle -1\) meredekségű egyenesen. Nyilván \(\displaystyle H(-5;3)\), a keresett \(\displaystyle e\) egyenes egyenlete \(\displaystyle y=x+8\), az \(\displaystyle A\) pont tükörképe pedig \(\displaystyle A'(-8;6)\). Mivel az \(\displaystyle AC\) szakasz felezőpontjának kordinátái (\(\displaystyle -3;5\)), így ez a pont rajta van az \(\displaystyle e\) egyenesen, tehát ez lesz a legkisebb kerületű négyszög negyedik csúcsa. A kerület ekkor:

\(\displaystyle AB+BC+CD+DA=AB+BC+CD+DA'=AB+BC+CA'=4+4+\sqrt{2^2+10^2}=8+\sqrt{104}=8+2\sqrt{26}\approx 18,198.\)

Statistics:

365 students sent a solution.
5 points:	103 students.
4 points:	102 students.
3 points:	51 students.
2 points:	27 students.
1 point:	35 students.
0 point:	45 students.
Unfair, not evaluated:	2 solutionss.

Problems in Mathematics of KöMaL, September 2011