Problem C. 1213. (February 2014)

C. 1213. Given a rectangle, construct a rectangle of half the area inside it such that the region between the two rectangles forms a frame of uniform width around the small rectangle.

(5 pont)

Deadline expired on March 10, 2014.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Legyen a téglalap két oldala \(\displaystyle a<b\), a keret szélessége pedig \(\displaystyle x\). Ekkor a belső téglalap oldalai \(\displaystyle a-2x\) és \(\displaystyle b-2x\), így a területekre felírható a következő egyenlet:

\(\displaystyle 2(a-2x)(b-2x)=ab,\)

\(\displaystyle 2(ab-2xb-2xa+4x^2)=ab,\)

\(\displaystyle 8x^2-4(a+b)x+ab=0,\)

\(\displaystyle x=\frac{4(a+b)\pm\sqrt{16(a+b)^2-32ab}}{16}= \frac{a+b\pm\sqrt{a^2+b^2}}{4}.\)

A két gyök közül a nagyobbik esetén az \(\displaystyle x>a/2\) lesz, tehát a keret nem jön létre:

\(\displaystyle \frac{a+b+\sqrt{a^2+b^2}}{4}>\frac a2,\)

\(\displaystyle \frac{b+\sqrt{a^2+b^2}}{4}>\frac a4,\)

amit 4-gyel beszorozva épp a háromszög-egyenlőtlenséget kapjuk a téglalap \(\displaystyle a\) és \(\displaystyle b\) oldala által meghatározott derékszögű háromszögre. (A műveletek megfordíthatók.)

Mivel \(\displaystyle (a+b)^2=a^2+b^2+2ab>a^2+b^2\), ezért a kisebbik gyök pozitív. Másrészt

\(\displaystyle \frac{a+b-\sqrt{a^2+b^2}}{4}<\frac a2,\)

hiszen ezt 4-gyel beszorozva majd átrendezve ismét egy háromszög-egyenlőtlenséget kapunk a téglalap \(\displaystyle a\) és \(\displaystyle b\) oldala által meghatározott derékszögű háromszögre (a műveletek itt is megfordíthatók):

\(\displaystyle b<a+\sqrt{a^2+b^2}.\)

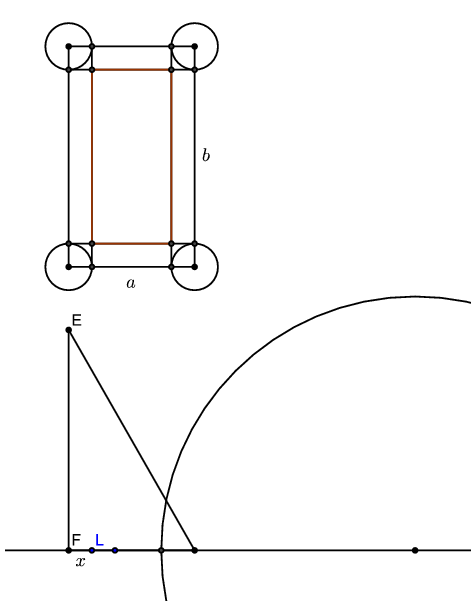
A kisebbik gyököt pedig úgy szerkeszthetjük meg, hogy rajzolunk egy \(\displaystyle a\) és \(\displaystyle b\) oldalú derékszögű háromszöget, ennek átfogója \(\displaystyle \sqrt{a^2+b^2}\). Egy egyenesen egymás mellé felmérjük az \(\displaystyle a\) és a \(\displaystyle b\) szakaszt, majd a \(\displaystyle \sqrt{a^2+b^2}\) szakaszt az ellenkező irányba mérjük fel. Az így kapott \(\displaystyle a+b-\sqrt{a^2+b^2}\) hosszú szakaszt negyedeljük, így megkapjuk \(\displaystyle x\)-et. A téglalap csúcsaiba \(\displaystyle x\) sugarú köröket rajzolunk. A körök a téglalap oldalait összesen nyolc pontban metszik. A megfelelő pontokat összekötve megkapjuk a belső téglalapot.

Statistics:

124 students sent a solution.
5 points:	Bottlik Judit, Döbröntei Dávid Bence, Eper Miklós, Erdei Ákos, Farkas Dóra, Kasó Ferenc, Klász Viktória, Kocsis Júlia, Kovács Péter Tamás, Krisztián Jonatán, Mészáros 01 Viktória, Nagy 102 Kinga, Nagy 911 Viktória, Regős Krisztina, Széles Katalin, Telek Máté László, Temesvári Fanni, Zsiros Ádám.
4 points:	51 students.
3 points:	25 students.
2 points:	8 students.
1 point:	16 students.
0 point:	5 students.
Unfair, not evaluated:	1 solutions.

Problems in Mathematics of KöMaL, February 2014