Problem C. 1398. (January 2017)

C. 1398. A cube is inscribed in a right circular cone: one face lies on the base of the cone, and the remaining four vertices are on the lateral surface of the cone. What is the surface area of the cube if the base radius of the cone is \(\displaystyle \frac{\sqrt{3}}{2}\,\), and its slant height is three times as large?

(5 pont)

Deadline expired on February 10, 2017.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Az ábrán látható metszetet úgy kaptuk, hogy a vízszintesen álló kúpot olyan függőleges síkkal metszettük el, amely átmegy a kocka vízszintes lapjainak egy-egy lapátlóján. Használjuk az ábra jelöléseit. A négyzet oldala legyen \(\displaystyle 2x\).

Az adatok alapján felírható, hogy \(\displaystyle PM=r=\frac{\sqrt3}{2}\), \(\displaystyle PR=a=3r\), \(\displaystyle EA=2x\), AM=\(\displaystyle \sqrt2x\).

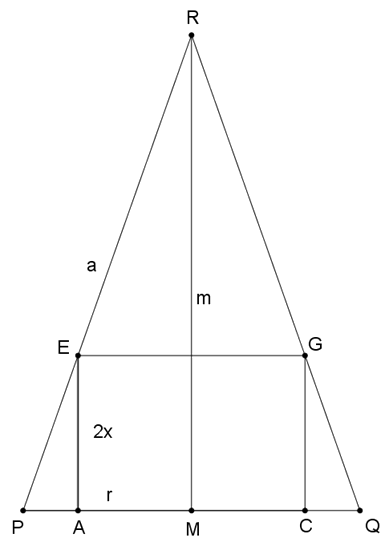
Felírva a Pitagorasz-tételt a \(\displaystyle PMR\) derékszögű háromszögben, majd behelyettesítve a helyébe \(\displaystyle 3r\)-et, végül a pozitív kifejezésekből gyököt vonva:

\(\displaystyle m^2=a^2-r^2,\)

\(\displaystyle m^2=9r^2-r^2=8r^2,\)

\(\displaystyle m=\sqrt8 r.\)

A \(\displaystyle PMR\) és a \(\displaystyle PAE\) derékszögű háromszögek hasonlóak, így \(\displaystyle \frac{RM}{PM}=\frac{EA}{PA}=\frac{EA}{PM-AM}\).

Itt is behelyettesítve majd rendezve:

\(\displaystyle \frac{m}{r}=\frac{2x}{r-\sqrt2 x},\)

\(\displaystyle \frac{\sqrt8 r}{r}=\frac{2x}{r-\sqrt2 x},\)

\(\displaystyle \sqrt8\cdot(r-\sqrt2 x)=2x,\)

\(\displaystyle \sqrt8 r-4x=2x,\)

\(\displaystyle \sqrt8 r=3\cdot(2x),\)

\(\displaystyle 2x=\frac{\sqrt8}{3} r.\)

A kocka felszíne:

\(\displaystyle A=6\cdot(2x)^2=6\cdot\frac89 r^2=\frac{16}{3}\cdot\frac34=4.\)

Statistics:

61 students sent a solution.
5 points:	Agócs Katinka, Balbisi Mirjam, Berényi Richárd, Bőzsöny András, Csapó Márton, Dankowsky Anna Zóra, Demeter Bianka Vivien, Édes Lili, Galvács Ákos, Horváth 31 László, Horváth 546 János, Kassai Levente, Kis 999 Alexandra, Kocsis Júlia, Kormányos Hanna Rebeka, Mácz Andrea, Nagy 911 Viktória, Nagy Olivér, Németh Csilla Márta, Pap-Takács Noémi, Pszota Máté, Pusztai Bertalan, Rittgasszer Ákos, Sipos Fanni Emma, Surján Anett, Szabó Dorottya, Szécsi Adél Lilla, Szentistványi István János, Szilágyi Éva, Szűcs 865 Eszter, Takács 666 Réka, Tanács Viktória, Wolff Vilmos, Zsombó István.
4 points:	Veres Károly.
3 points:	18 students.
2 points:	5 students.
1 point:	1 student.
0 point:	2 students.

Problems in Mathematics of KöMaL, January 2017