Problem C. 998. (September 2009)

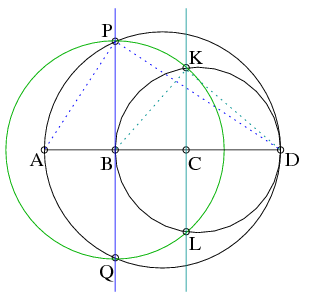
C. 998. The points A, B, C and D lie on a line in this order, and AB=BC. Draw perpendiculars to AD at B and C. The perpendicular drawn at B intersects the circle of diameter AD at P and Q. The perpendicular drawn at C intersects the circle of diameter BD at K and L. Show that the centre of the circle passing through points P, K, L and Q is point B.

(5 pont)

Deadline expired on October 12, 2009.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. A feladatbeli egyenesek, körök, metszéspontok mind szimmetrikusak az \(\displaystyle AD\) egyenesre (mert \(\displaystyle PQ\) és \(\displaystyle KL\) egyenese merőleges \(\displaystyle AD\)-re, a köröknek pedig centrálisa.) Legyenek \(\displaystyle AB=BC=a\) és \(\displaystyle CD=b\) a szakaszok hosszai. Így \(\displaystyle AD=2a+b\) és \(\displaystyle BD=a+b\) az átmérők. Az \(\displaystyle APD\) háromszög és a \(\displaystyle BKD\) háromszög derékszögű (Thálesz-tétel). Az \(\displaystyle APB\) háromszögben \(\displaystyle PB\) magasság a feladat szerint, és a magasság-tételt felírva \(\displaystyle PB=\sqrt{AB \cdot BD}=\sqrt{a(a+b)}\). \(\displaystyle BKD\) háromszögben a befogótételt használva \(\displaystyle BK=\sqrt{BC \cdot CD}=\sqrt{a(a+b)}\). Tehát \(\displaystyle BP=BK\) és a szimmetria miatt \(\displaystyle BP=BL=BQ\), azaz \(\displaystyle P\), \(\displaystyle K\), \(\displaystyle L\), \(\displaystyle Q\) pontok mind ugyanakkora távolságra vannak \(\displaystyle B\)-től, azaz a \(\displaystyle B\) középpontú \(\displaystyle \sqrt{a(a+b)}\) sugarú körben \(\displaystyle PKLQ\) húrnégyszög.

Statistics:

292 students sent a solution.
5 points:	152 students.
4 points:	58 students.
3 points:	5 students.
2 points:	4 students.
1 point:	14 students.
0 point:	58 students.
Unfair, not evaluated:	1 solutions.

Problems in Mathematics of KöMaL, September 2009