Problem K. 75. (February 2006)

K. 75. The point K lies on each of the circles of radius r centred at the points K₁, K₂, K₃. The other common points of two of the three circles are P, Q, and R. Show that the triangles K₁K₂K₃ and PQR are congruent.

(6 pont)

Deadline expired on March 10, 2006.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás:

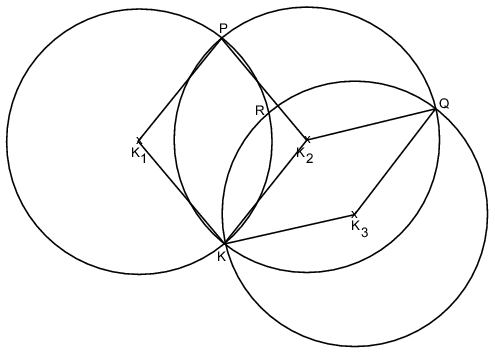
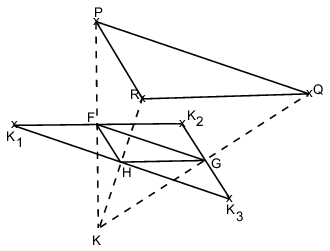
Használjuk az ábrák jelöléseit! Ha két egyforma sugarú kör metszi egymást két pontban, akkor a körök középpontjai és metszéspontjai egy rombuszt alkotnak, a kétirányú tengelyes szimmetria miatt. Ennek megfelelően (az ábra jelöléseit használva) a K₁KK₂P négyszög rombusz, tehát K₁K₂ és KP szakaszok kölcsönösen merőlegesen felezik egymást. Hasonlóan K₂K₃ és KQ, valamint K₁K₃ és KR szakaszok is. A megfelelő felezőpontokat jelölje F, G, H. Innen kétféleképpen lehet befejezni.

I. befejezés: A korábban mondottak miatt a PRK háromszögben FH középvonal, tehát párhuzamos PR-rel és feleakkora, mint PR. Ugyanakkor FH középvonal a K₁K₂K₃ háromszögben is, tehát párhuzamos K₂K₃-mal és feleakkora, mint K₂K₃. Ebből következik, hogy PR párhuzamos és egyenlő K₂K₃-mal, Hasonlóan mutatható meg, hogy PQ párhuzamos és egyenlő K₁K₃-mal és QR párhuzamos és egyenlő K₂K₁-gyel. Tehát a K₁K₂K₃ háromszög és a PQR háromszög egybevágók, mert megfelelő oldalaik egyenlők (és párhuzamosak is).

II. befejezés: Az elmondottakból következően az FGH háromszöget a K pontból kétszeresére nagyítva a PQR háromszöget kapjuk. Mivel FGH a K₁K₂K₃ háromszög középvonalai által alkotott háromszög, ezért ahhoz hasonló, és a hasonlóság aránya 1/2. (A hasonlóság középpontja a K₁K₂K₃ háromszög súlypontja.) Tehát a K₁K₂K₃ háromszög és a PQR háromszög egybevágók. (A K₁K₂K₃ háromszöget a súlypontjából 1/2 arányban kicsinyítjük, majd a kapott háromszöget K-ból kétszeresére nagyítjuk, és így kapjuk a PQR háromszöget.)

Statistics:

92 students sent a solution.
6 points:	Bencs 111 Ferenc, Bereczki 118 Katalin, Berinkei Ottó, Besnyő Réka, Bihari Mónika, Borbás Bence, Boros Csanád Örs, Csányi János Dániel, Cseresznyék Dávid, Czapf Anna, Dániel Balázs, Egyed Zsombor, Englert Dávid, Erdész Zsombor Bálint, Horváth 003 Péter, Huszár Kristóf, Iván Dávid, Király Csilla, Kovács 007 Attila, Kunos Ádám, Kurgyis Kata, Lantos Tamás, Lenzsér Gábor, Meszlényi Regina, Molnár 289 András, Németh Erika Judit, Petróczy Dóra Gréta, Róka Péter, Schlarb Krisztián, Solymos Tamás, Szepesvári Dávid, Szikszay László, Zsupanek Alexandra.
5 points:	Ballér Krisztián, Márki Róbert.
4 points:	5 students.
3 points:	6 students.
2 points:	5 students.
1 point:	5 students.
0 point:	33 students.
Unfair, not evaluated:	3 solutionss.

Problems in Mathematics of KöMaL, February 2006