Problem P. 4939. (May 2017)

P. 4939. A ball was projected at point \(\displaystyle A\) and it hit a wall at point \(\displaystyle B\) horizontally. From \(\displaystyle B\) the ball ``flies'' to the points \(\displaystyle C_1, C_2, \dots,\) and finally gets back to point \(\displaystyle A\). The coefficient of restitution is \(\displaystyle \varepsilon\) at any point. Find \(\displaystyle \varepsilon\), if the ball does not bounce up at all when it gets back to point \(\displaystyle A\).

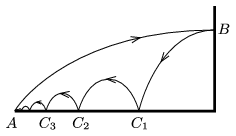
(It can be assumed that the air-drag exerted on the ball is negligible and the ball does not start rotating.)

(5 pont)

Deadline expired on June 12, 2017.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Legyen a kilőtt golyó sebességének vízszintes komponense \(\displaystyle u_0\), a függőleges komponense pedig \(\displaystyle v_0\). A golyó a falat (a \(\displaystyle B\) pontot) \(\displaystyle t_0=v_0/g\) idő alatt éri el, és

\(\displaystyle H=\frac{1}{2}v_0t_0=\frac{v_0^2}{2g}\)

magasra emelkedik. Ezalatt

\(\displaystyle d=u_0t_0=\frac{u_0 v_0}{g}\)

utat tesz meg vízszintesen, ez tehát az \(\displaystyle A\) pont és a fal távolsága.

A falról a golyó \(\displaystyle \varepsilon u_0\) sebességgel pattan vissza, és ez a vízszintes sebességkomponense a továbbiakban már nem változik. A golyó \(\displaystyle t_1=v_0/g\) idő alatt esik vissza a talaj szintjére, vízszintesen tehát

\(\displaystyle d_1=\varepsilon u_0t_1=\varepsilon \frac{u_0 v_0}{g}\)

az elmozdulása, függőleges sebességének nagysága pedig \(\displaystyle v_0\) lesz.

A talajról visszapattanó labda függőleges sebességkomponense \(\displaystyle \varepsilon v_0\), a következő pattanásig \(\displaystyle t_2=2\varepsilon v_0/g\) idő alatt vízszintes irányban

\(\displaystyle d_2=2\varepsilon^2 \frac{u_0 v_0}{g}\)

távolságnyit mozdul el.

A további pattanások során a függőleges sebességkomponens mindig az előző érték \(\displaystyle \varepsilon\)-szorosára csökken, és ugyanilyen arányban csökken a pattanások közötti vízszintes irányú elmozdulás is:

\(\displaystyle d_3= 2\varepsilon^3 \frac{u_0 v_0}{g},\quad d_4= 2\varepsilon^4 \frac{u_0 v_0}{g}, \ldots , d_n= 2\varepsilon^n \frac{u_0 v_0}{g}.\)

A golyó nagyon sok (\(\displaystyle n\rightarrow \infty\)) pattanás után, amikor a függőleges sebessége már nullára csökken, visszaérkezik az \(\displaystyle A\) pontba. A

\(\displaystyle d_1+d_2+d_3+\ldots =d\)

feltételből az

\(\displaystyle 1=\varepsilon+2\varepsilon^2+2\varepsilon^3+2\varepsilon^4+\ldots=\varepsilon+\frac{2\varepsilon^2}{1-\varepsilon}\)

egyenletet kapjuk, amelynek (fizikailag reális, pozitív) megoldása:

\(\displaystyle \varepsilon=\sqrt{2}-1\approx 0{,}41.\)

Megjegyzés. Ha \(\displaystyle \epsilon>\sqrt{2}-1\), akkor a golyó pattogása már az \(\displaystyle A\) pontba történő visszaérkezése előtt megszűnik.

Statistics:

45 students sent a solution.
5 points:	Bartók Imre, Bekes Nándor, Bíró Dániel, Bukor Benedek, Csire Roland, Csuha Boglárka, Debreczeni Tibor, Elek Péter, Fekete Balázs Attila, Jakus Balázs István, Jánosik Áron, Kavas Katalin, Kolontári Péter, Kozák András, Krasznai Anna, Makovsky Mihály, Mamuzsics Gergő Bence, Marozsák Tóbiás , Molnár 957 Barnabás, Molnár Mátyás, Morvai Orsolya, Nagy 555 Botond, Ónodi Gergely, Páhoki Tamás, Paulovics Péter, Pécsi 117 Ildikó, Póta Balázs, Szentivánszki Soma , Tófalusi Ádám, Tóth 111 Máté , Turcsányi Ádám, Zöllner András.
4 points:	Berke Martin, Édes Lili, Jánosdeák Márk, Olosz Adél, Pszota Máté, Sal Dávid, Varga-Umbrich Eszter.
3 points:	2 students.
2 points:	1 student.
1 point:	3 students.

Problems in Physics of KöMaL, May 2017