KöMaL Problems in Mathematics, April 2005
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'C'Deadline expired on May 17, 2005. |
C. 805. Find all sets of three integers, such that their product is four times their sum, and one number is twice the sum of the other two.
(5 pont)
solution (in Hungarian), statistics
C. 806. Find all positive integers divisible by 7 that end in 5 in the decimal notation and the rest of their digits are 1.
(5 pont)
solution (in Hungarian), statistics
C. 807. The lengths of two adjacent sides of a quadrilateral are 2 units and 1 unit, and they enclose an angle of 60o. The quadrilateral is cyclic and it is also a tangent quadrilateral. What are the lengths of the other two sides?
(5 pont)
solution (in Hungarian), statistics
C. 808. Solve the equation {3x}2+{x}2=1.
(5 pont)
solution (in Hungarian), statistics
C. 809. The midpoint of the edge AE of the unit cube ABCDEFGH is P, and the midpoint of the face BCGF is R.
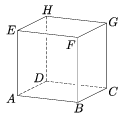
a) Find the area of the intersection of the cube with the plane through the points P, B, R.
b) The above plane cuts the cube into two solids. What is the ratio of the volumes of the two parts?
(5 pont)
 |
Problems with sign 'B'Deadline expired on May 17, 2005. |
B. 3812. Find all positive integers n, such that
a) 7399|n! , but 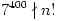 , and
, and
b) 7400|n! , but 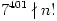 .
.
(4 pont)
solution (in Hungarian), statistics
B. 3813. Prove that there is exactly one single point M inside an arbitrary triangle ABC, such that
MA+BC=MB+AC =MC+AB.
(4 pont)
solution (in Hungarian), statistics
B. 3814. n and k are positive integers, such that 2kn|k2+n2-k. Prove that k is a square number.
(4 pont)
solution (in Hungarian), statistics
B. 3815. A plane intersects each line segment of a closed polygon P1P2...PnP1 of the space. The intersection with the line segment PiPi+1 is the interior point Qi. Prove that
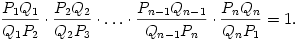
(3 pont)
solution (in Hungarian), statistics
B. 3816. The centre of the inscribed circle of the triangle ABC is O. The extensions of the line segments AO, BO, CO beyond O intersect the circumscribed circle at A1, B1, C1, respectively. Prove that the area of the triangle A1B1C1 is
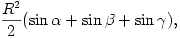
where R is the radius of the circumscribed circle, and  ,
,  ,
,  are the angles of the original triangle ABC.
are the angles of the original triangle ABC.
(4 pont)
solution (in Hungarian), statistics
B. 3817. The sequence an is defined as follows:
a1 2,
2, 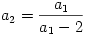 ,
, 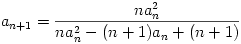 , if n
, if n 2.
2.
Prove that the inequality
a1+2a2+3a3+...+nan=a1.a2.a3.....an
is true for all n.
(5 pont)
solution (in Hungarian), statistics
B. 3818. The length of all three edges from a certain vertex of a tetrahedron is unity, and they pairwise enclose 45 angles. Find the volume of the tetrahedron. (based on the idea of
(4 pont)
solution (in Hungarian), statistics
B. 3819. Show that if A1B1, A2B2 and A3B3 are three parallel chords of a circle, then the perpendiculars dropped from the point A1, A2 and A3 onto the line B2B3, B3B1 and B1B2, respectively, are concurrent.
(5 pont)
solution (in Hungarian), statistics
B. 3820. Solve the following equation:
(5x-2x-2)2+ 2lg (5x+2x-2)=x.
(4 pont)
solution (in Hungarian), statistics
B. 3821. a, b, c are positive numbers, such that a2+b2+c2=1. Find the smallest possible value of the sum
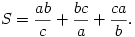
(5 pont)
 |
Problems with sign 'A'Deadline expired on May 17, 2005. |
A. 371. Given that a+b c+1, b+c
c+1, b+c  a+1, c+a
a+1, c+a b+1 for the numbers a,b,c
b+1 for the numbers a,b,c  0, show that a2+b2+c2
0, show that a2+b2+c2 2abc+1.
2abc+1.
(5 pont)
A. 372. An equilateral triangle of side n is divided into equilateral triangles of unit side. How many castles can be placed on the lattice points of the triangular lattice obtained so that no two of them attack each other? Castles can move parallel to the sides of the triangle, in six directions altogether. (Suggested by A. Egri, Hajdúszoboszló)
(5 pont)
A. 373. P is a point in the interior of the quadrilateral A1A2A3A4 that does not lie on either diagonal. The points Bi lie in the interior of each line segment AiP. Let Cij be the intersection of the lines AiBj and AjBi (1 i<j
i<j  4). Prove that the line segments C12C34, C13C24, C14C23 are all concurrent.
4). Prove that the line segments C12C34, C13C24, C14C23 are all concurrent.
(5 pont)
Upload your solutions above.
