KöMaL Problems in Mathematics, April 2006
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'C'Deadline expired on May 18, 2006. |
C. 850. An arbitrary interior point of a regular hexagon of unit side is reflected about the midpoint of each side, respectively. Calculate the area of the resulting hexagon.
(5 pont)
solution (in Hungarian), statistics
C. 851. A fair coin is tossed 12 times in a row and the outcomes are listed. How many sequences of outcomes are possible in which there are no two consecutive heads?
(5 pont)
solution (in Hungarian), statistics
C. 852. Solve the following inequality on the set of real numbers: .
(5 pont)
solution (in Hungarian), statistics
C. 853. Consider four rays in the space starting from a common point and enclose pairwise equal non-zero angles. What is that angle?
(5 pont)
solution (in Hungarian), statistics
C. 854. Prove that the following equality is true for every positive integer n:
(5 pont)
 |
Problems with sign 'B'Deadline expired on May 18, 2006. |
B. 3902. P is an interior point of the triangle ABC. The perimeter of the triangle is 2s. Show that s<PA+PB+PC<2s.
(3 pont)
solution (in Hungarian), statistics
B. 3903. Solve the following equation:
(3 pont)
solution (in Hungarian), statistics
B. 3904. ABC is an isosceles triangle. Drop a perpendicular from the midpoint D of the base BC onto the leg AC and denote the foot of the perpendicular by E. The midpoint of the line segment DE is F. Show that the lines BE and AF are perpendicular.
(4 pont)
solution (in Hungarian), statistics
B. 3905. How many solutions does the equation y2=x2-x+1 have in the set of a) integers; b) rational numbers?
(5 pont)
solution (in Hungarian), statistics
B. 3906. The skew lines e and f are perpendicular. The unit line segment AB has its endpoint A on e and endpoint B on f. What is the locus of the midpoint of AB as its endpoints are moving along the lines?
(4 pont)
solution (in Hungarian), statistics
B. 3907. Solve the following equation: sin x+cos x+sin xcos x=1.
(3 pont)
solution (in Hungarian), statistics
B. 3908. Prove that 23n+1 is divisible by 3n+1 for all real numbers n.
(3 pont)
solution (in Hungarian), statistics
B. 3909. A fair coin is tossed 12 times in a row and the outcomes are listed. What is the probability that there are no three consecutive heads?
(5 pont)
solution (in Hungarian), statistics
B. 3910. AB is a diameter in the circle k. Choose an arbitrary point E in the interior of the circle. The other intersections of the lines AE and BE with the circle are C and D, respectively. Prove that the value of the expression AC.AE+BD.BE is independent of the position of E.
(4 pont)
solution (in Hungarian), statistics
B. 3911. Prove that it is possible to inscribe an ellipse in any acute triangle, such that the foci are the orthocentre and the circumcentre of the triangle, respectively.
(5 pont)
 |
Problems with sign 'A'Deadline expired on May 18, 2006. |
A. 398. Given a circle k in the plane and a line  lying outside k. Moreover, a point O is given on the circle. Define the binary operator + on the points of k as follows. For arbitrary points X and Y, denote by MXY the intersection point of lines XY and
lying outside k. Moreover, a point O is given on the circle. Define the binary operator + on the points of k as follows. For arbitrary points X and Y, denote by MXY the intersection point of lines XY and  . (If X=Y then take the tangent. If the lines are parallel then MXY is the ideal point.) Construct the second intersection of OMXY and k. (If the line is the tangent at O then also the second intersection is O.) Denote this point by X+Y (see the figure).
. (If X=Y then take the tangent. If the lines are parallel then MXY is the ideal point.) Construct the second intersection of OMXY and k. (If the line is the tangent at O then also the second intersection is O.) Denote this point by X+Y (see the figure).
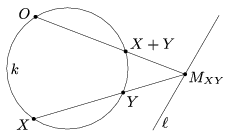
Show that operation + can be extended to the union of k,  and the ideal point of
and the ideal point of  such that the points with this operation form an Abelian group with the unity O; i.e. the operation has the following properties:
such that the points with this operation form an Abelian group with the unity O; i.e. the operation has the following properties:
a) (X+Y)+Z=X+(Y+Z) for all points X, Y, Z;
b) X+Y=Y+X for all points X, Y;
c) X+O=X for all points X;
d) For an arbitrary point X there exists a point Y such that X+Y=O.
(5 pont)
A. 399. Given n 3-element subset of a certain set S. Prove that if n=6 then the elements of S can be colored with two colors such that each subset contains both colors. Is the same true for n=7?
(5 pont)
A. 400. Prove that
for all real numbers x, y, z, u.
(5 pont)
Upload your solutions above.
