KöMaL Problems in Mathematics, May 2006
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'C'Deadline expired on June 15, 2006. |
C. 855. We need a 60o angle, but we have no other materials but a rectangular sheet of paper. We first fold the rectangle in half along one of its bimedians. Then fold up one corner along a line through an adjacent corner, so that the vertex be on the bimedian (as shown in the Figure). Show that the acute angle of the trapezium hence obtained is 60o.
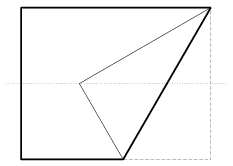
(5 pont)
solution (in Hungarian), statistics
C. 856. Find all natural numbers n, such that
5n+12n2+12n+3
is divisible by 100.
(5 pont)
solution (in Hungarian), statistics
C. 857. Find the pairs (c,d) for which the equation x3-8x2+cx+d=0 has three (not necessarily) different positive integer roots.
(5 pont)
solution (in Hungarian), statistics
C. 858. The perimeter and the area of a rectangle are equal to the perimeter and the area of a rhombus, respectively, that has an angle of 30o. Find the ratio of the sides of the rectangle.
(5 pont)
solution (in Hungarian), statistics
C. 859. Prove that the equality
holds in every triangle.
Suggested by G. Holló, Budapest
(5 pont)
 |
Problems with sign 'B'Deadline expired on June 15, 2006. |
B. 3912. Prove that every convex quadrilateral has a vertex, such that its reflection about the midpoint of the line segment connecting the two adjacent vertices does not lie outside the quadrilateral.
(4 pont)
solution (in Hungarian), statistics
B. 3913. Consider the following two number sets:
How many elements are there in the set A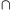 B?
B?
(3 pont)
solution (in Hungarian), statistics
B. 3914. P is an arbitrary point on the side AB of the parallelogram ABCD, and Q is an arbitrary point of side CD. Let M denote the intersection of the lines DP and AQ, and let N denote the intersection of the lines CP and BQ. Show that the line MN is passing through the centre of the parallelogram.
(4 pont)
solution (in Hungarian), statistics
B. 3915. Each side of the triangle ABC is divided into p equal parts, where p is a prime number. Then one point of division on each side is connected to the opposite vertex so that the three connecting lines are concurrent. Determine the possible values of p.
(4 pont)
solution (in Hungarian), statistics
B. 3916. Prove that the inequality
holds for all positive numbers x, y.
(3 pont)
solution (in Hungarian), statistics
B. 3917. Prove that an open interval of length may contain at most
rational numbers whose denominator is at most n.
(5 pont)
solution (in Hungarian), statistics
B. 3918. Find the solutions of the equation
cos 4x-tan 5x=cot 5x-sin 6x
in the interval (-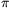 ;
;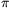 ).
).
(4 pont)
solution (in Hungarian), statistics
B. 3919. Construct a point P in the interior of an acute-angled triangle ABC, such that PA.BC=PB.CA=PC.AB.
Suggested by G. Holló, Budapest
(3 pont)
solution (in Hungarian), statistics
B. 3920. Solve the equation 3x+4y=5z in the set of positive integers.
(5 pont)
solution (in Hungarian), statistics
B. 3921. A convex solid is built out of four regular hexagons of unit side and four regular triangles. Prove that a sphere can be circumscribed about the solid, and find the radius of the sphere.
(5 pont)
 |
Problems with sign 'A'Deadline expired on June 15, 2006. |
A. 401. ABCD is a tetrahedron. The insphere touches the face ABC at H. The exsphere opposite D (which also touches the face ABC and the three planes containing the other faces) touches the face ABC at O. If O is the circumcenter of ABC, show that H is the orthocenter of ABC.
Polish competition problem
(5 pont)
A. 402. Two players play the following game: Let n be a fixed integer greater than 1. Starting from number k=2, each player has two possible moves: either replace the number k by k+1 or by 2k. The player who is forced to write a number greater than n loses the game. Which player has a winning strategy for which n?
Vojtech Jarnik Competition,Ostrava, 2006
(5 pont)
A. 403. Find all positive integers n for which the equation has a solution in positive integers.
Vietnamise competition problem
(5 pont)
Upload your solutions above.
