KöMaL Problems in Physics, September 2006
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'M'Deadline expired on October 11, 2006. |
M. 271. An inclined plane is placed to the table next to the edge of the table. Where does the ball, which rolls down the plane, hit the ground? (The angle of elevation of the plane can be varied.) Consider the following two cases:
a) the ball on the plane covers the same constant distance of l;
b) the ball on the plane starts at the same hight of h.
Find the angle 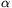 at which the ball hits the ground at the furthest point.
at which the ball hits the ground at the furthest point.
(6 pont)
 |
Problems with sign 'P'Deadline expired on December 11, 2006. |
P. 3904. The volume of a rubber ball is 600 cm3. When it floats on the surface of water 80% of its volume is above the water. a) Find the average density of the ball. b) If the ball is pushed down, and immersed in the water, what is the force with which it can be kept under the water?
(3 pont)
solution (in Hungarian), statistics
P. 3905. A body is hanging on a spring attached to the ceiling of an elevator. Suddenly the lift starts moving and then it moves with a constant upward speed. How does the elongation of the spring change?
(4 pont)
solution (in Hungarian), statistics
P. 3906. A 2-kg brick falls 5 m and then a worker catches it and brings it into rest in a distance of 0.5 m exerting an upward constant force. a) Find the force exerted by the worker. b) Find the average power of the worker.
(4 pont)
solution (in Hungarian), statistics
P. 3907. Estimate how much more it costs to cover the distance by car between Miskolc and Sárospatak if the lights are on than if they are turned off. The total power dissipated in the lights is 50 W, the average speed is 60 km/h and the efficiency of the engine is 25%.
(4 pont)
solution (in Hungarian), statistics
P. 3908. A solar furnace is a huge concave mirror which is always turned towards the Sun. A piece of metal, which is to be melted, is placed to the focus of the mirror. What can be the greatest temperature at the focus of the solar furnace?
(5 pont)
solution (in Hungarian), statistics
P. 3909. How would you connect the capacitors whose capacitances are 1 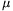 F, 2
F, 2 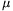 F, 3
F, 3 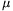 F and 4
F and 4 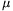 F, such that their equivalent capacitance is 1
F, such that their equivalent capacitance is 1 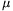 F?
F?
(4 pont)
solution (in Hungarian), statistics
P. 3910. Calculate the current that flows through the battery shown in the figure. Find the resistor in which the dissipated power is the greatest.

(4 pont)
P. 3911. A point-like charge undergoes uniform circular motion around another fixed, point-like charge of opposite charge. Find the potential energy of the moving charge in terms of its kinetic energy. Calculate the ratio of the total energy and the kinetic energy.
(4 pont)
solution (in Hungarian), statistics
P. 3912. Two long straight wires are hanged by 1.2-m long insulating threads as shown in the figure. A 1-m long piece of both wires has the mass of 20 g. The currents have the same magnitude in the wires. Find the current in the wires if the angle between the threads is 2o. What is the direction of the currents?
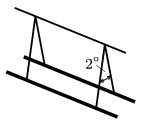
(4 pont)
Upload your solutions above.
