KöMaL Problems in Physics, January 2007
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'M'Deadline expired on February 12, 2007. |
M. 275. Let a small disc of magnet slide along a long inclined plane made of aluminum. Measure the speed of the disc when it is uniform as a function of the angle of inclination of the slope. Determine the coefficient of kinetic friction.
(6 pont)
 |
Problems with sign 'P'Deadline expired on February 12, 2007. |
P. 3943. John showed his friends that with his glasses he can collect the Sun's rays and light a piece of paper. When the Sun is shining why don't his glasses burn the skin near his eyes?
(3 pont)
P. 3944. A spiral spring is hanged at one of its end such that its loops do not touch each other, and then it is connected to a voltage supply and current flows through it. Will the spring be compressed or stretched? What happens if it is connected to an alternating voltage supply?
(4 pont)
P. 3945. Find the elongation of that spring which pulls a cart of mass M with a constant force, and the mathematical pendulum which is attached to the cart makes an angle of  with the vertical. The mass of the bob on the pendulum is m and the spring constant is D. Friction and the mass of the spring are negligible.
with the vertical. The mass of the bob on the pendulum is m and the spring constant is D. Friction and the mass of the spring are negligible.
(4 pont)
P. 3946. An elevator cab, whose total mass with its passengers is 600 kg, ascends uniformly. The mass of the counterweight is 300 kg. The mechanical power of the motor is 10 kW and the efficiency is 80%.
a) Find the speed of the lift.
b) Calculate the tension in the rope which pulls the lift.
(4 pont)
P. 3947. A spiral spring of negligible mass and spring constant D lies un-stretched on a smooth horizontal plane. Its length is l0, and one of its end is fixed to a vertical axle, while the to other a point-like disc of mass m is attached. Another disc of mass m collides elastically with the disc attached to the spring. The initial velocity of the moving disc is v and is perpendicular to the axis of the spring. Find the smallest radius of curvature of the path of the disc attached to the spring. Data: D=64 N/m, l0=1 m, m=0.5 kg, v=8 m/s.
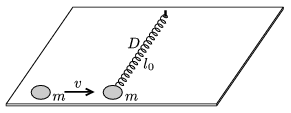
(5 pont)
P. 3948. A plane flies at a height of 10 km and the state of weightlessness is created for 20 seconds. The plane ascends for 10 seconds and then descends for 10 seconds and returns to the initial height of 10 km.
a) Calculate the angle of elevation at the beginning of the weightlessness, if the speed at this time is 900 km/h?
b) To what height does the plane ascend?
c) What is the speed of the plane at the highest point?
(4 pont)
P. 3949. What is the period of that space probe which orbits a 100 km above the surface of the Mars. For how long can the space probe, ``see'', remain in radio-contact with the lander? First the lander was bouncing on the surface of Mars, which has rare atmosphere. After the first bounce it raised 20 metres. What is the elapsed time between two bounces?
(4 pont)
P. 3950. A sample of nitrogen gas was taken through the cyclic process shown in the figure. By what factor is the energy released by the gas in the isochoric process is greater than the work done by the gas in the isobaric process?
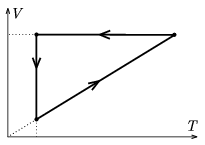
(4 pont)
P. 3951. Cloud droplets of diameter 0.01 mm are charged to a potential of 1 mV and unite into droplets of diameter 0.1 mm. What is the voltage of this new droplet? By what factor is the speed of fall of the big droplet greater than the that of the small one?
(4 pont)
P. 3952. The back wall of an aquarium has a reflective surface and it is 30 cm from the front wall. The width of the walls is negligible. A fish swims in the water exactly halfway between the two walls. The fish is observed from a direction which is perpendicular to the walls. a) How far from the front wall do you see the fish? b) How far do you see the image of the fish? The refractive index of water is 1.33.
(4 pont)
Upload your solutions above.
