Problems in Physics, February 2007

M. 276. Measure how the time while the sand runs to the bottom bulb of an hourglass change if you vary the angle between the symmetry axis of the hourglass and the vertical.

(6 points)

P. 3953. In a pot there is salt water of weight 40 N, and an object weighing 60 N is floating in it. Find the area of the base of the pot if the height of the water in it is 25 cm. The weight of 1 l salt water is 10 N.

(3 points)

P. 3954. Cars of length l travel with uniform velocity of v and pass a road sign. The distance between them is x. The greater their speed the greater the distance between them. The relationship between their speed and the distance between them is given by the function x=v², where is constant, characteristic to all cars. What is the velocity at which the most cars go past the road sign during a given time?

(4 points)

P. 3955. There are two samples of gas in a thermally insulated cylinder. One of them is Argon at a temperature of 300 K, and the other is Nitrogen at a temperature of 400 K. There is a thermally insulated wall between them. The two gases have the same pressure and the same volume. Then the wall between the gases is taken away, and the two gases mix.

a) Does the energy of the system change?

b) What will be the common temperature?

c) How does the pressure change?

d) Does the entropy of the system change?

(5 points)

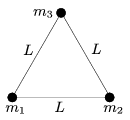
P. 3956. There are three small discs of masses m₁=0.2 kg, m₂=0.3 kg, m₃=0.52 kg on a horizontal air-cushioned table, and they are tied with thin massless threads of length L=60 cm, as shown in the figure. a) Find the distances between any of the discs and the centre of mass of the system. b) The system is made to rotate about the centre of mass at a constant angular speed of 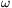=10 s^-1. Calculate the tensions in the threads.

(5 points)

P. 3957. Estimate the number of electrons which pass the cross section of the ring on the finger of the fan while he or she is waving on a rock-concert.

(4 points)

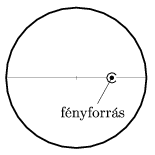
P. 3958. There is a point-like light-source in a metal sphere whose surface reflects light. The light-source is at the midpoint of a radius of the sphere. After two reflections where will be the image of the light-source if it is shaded as shown in the figure. Where will be the image if the shading-cap is rotated by 180^o? Draw a figure of the special rays too.

(4 points)

P. 3959. Estimate how far would the Earth move away from the Sun because of its radiation in a 100 years. The power of the radiation of the Sun is P=3.8^.10²⁶ W.

(5 points)

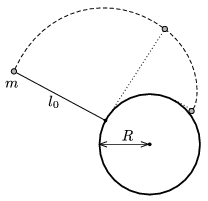
P. 3960. A vertical cylinder of radius R is fixed on a horizontal, ideally smooth tabletop. There is a string attached to the bottom of the cylinder, while to the other end of the string a small disc, whose mass is m, is fixed. The small disc is given a velocity v₀ which is perpendicular to the tightened string. The disc slides on the tabletop while the string is wound round the cylinder. a) What is the velocity of the small disc when it hits the wall of the cylinder? (Give both the direction and the magnitude.) b) What is the tension at this moment? (Data: R=1 m, l₀=2 m, r=2 cm, m=5 g.)

(5 points)

P. 3961. A beam of carbon ions of velocity 10 km/s is shot into magnetic field of 0.01 T, perpendicularly to the magnetic field. It is found that the ions move along two circular paths. The radii of the paths are 134 mm, and 124 mm. What is the mass of the two different ions? How do they differ from each other?

(4 points)

P. 3962. A 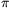⁺ meson of negligible initial velocity decays to a 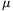⁺ (muon) and a neutrino. With what energy does the neutrino move?

(The rest mass of neutrino can be considered zero. The rest energy of the 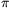⁺ meson is 140 MeV, and the rest energy of the muon is 106 MeV.)

(5 points)