KöMaL Problems in Physics, May 2007
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'M'Deadline expired on June 11, 2007. |
M. 279. On windy days the overhead tram wires can easily begin to swing. The period of the oscillation depends on how much the wires sag. Model the wire with a single chain of the given length, which swings. Measure for small amplitudes how the period depends on the sag of the chain.
(6 pont)
 |
Problems with sign 'P'Deadline expired on June 11, 2007. |
P. 3983. A racewalker on the training walked between point A and point B. First he walked from A to B taking 120 steps in each minute then he turned back at B and went back to A taking 90 steps in each minute. He turned back at A and went to B again and took 60 steps per minute, and finally he turned back at B and stepped only 45 in one minute until he got back to A. It took him 1 hour and 3 minutes. What is the distance in steps between the points A and B? What is the average steps that the walker took in one minute?
(3 pont)
P. 3984. Estimate how much does the height of the mercury column change in Torricelli's experiment
a) if the device is brought from the room of tempereture to the balcony where the temperature is
;
b) if the device is kept in the room but some drops of water is inserted into the tube.
(In his famous experiment Torricelli created a metre long tube sealed at the top end, filled it with mercury, and set it vertically into a basin of mercury. The column of mercury fell to about 76 cm.)
(4 pont)
P. 3985. Two objects of mass m are connected with a rope of length  as shown in the figure. The rope can slide in a tube which forms a quarter of a circle, and which is fixed to the edge of the table. Initially
as shown in the figure. The rope can slide in a tube which forms a quarter of a circle, and which is fixed to the edge of the table. Initially of the rope hangs vertically. Friction is negligible.
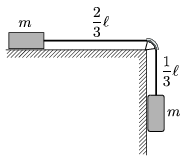
a) If the system is released, how long does it take for the object on the right handside to descend a distance of , and at that time what are the speeds of the objects?
b) What would be the speeds of the object after covering the same distance if the mass of the rope was m as well?
(4 pont)
P. 3986. A sample of ideal gas of 0.3 mol is taken through the cyclic process shown in the figure. The temperature of the gas at state 3 is 900 K, and at state 4 600 K.
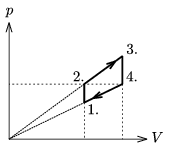
a) Find the temperature of the gas at states 1 and 2.
b) What is the work done by the gas during one cycle?
(4 pont)
P. 3987. A converging lens of focal length f is used to create a real image on a screen placed at a distance of d from the lens. Graph the number of possible images as a function of d.
(4 pont)
P. 3988. A small charged bead of mass m and of charge q can move on a frictionless horizontal rod. A pointlike charge Q whose charge is opposite the charge on the bead, is fixed at a point which is at a distance of d from the rod. The bead is a bit displaced from its equilibrium position and then released. Find the period of the resulted oscillatory motion.
Data: Q=10-8 C, q=-10-8 C, m=1 g, d=10 cm.
(5 pont)
P. 3989. A proton moving with 60% of the speed of light is scattered elastically on another proton which was initially at rest. After scattering the angles of deflection of the two protons measured from the direction of the motion of the initially moving proton are the same. What is this scattering angle and what are the speeds of the protons?
(5 pont)
P. 3990. If two uniform bodies are moved closer to each other along the line which joins them, then the gravitational force exerted between them usually increases. Is this always true? Give examples for the opposite.
(4 pont)
P. 3991. A solid cylinder of mass m and radius R is rotated with an angular speed of 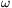 0 as shown in the figure and placed carefully to a long enough slope at a distance of s measured from the bottom of the slope. The incline angle is
0 as shown in the figure and placed carefully to a long enough slope at a distance of s measured from the bottom of the slope. The incline angle is  . How far from the bottom will the cylinder move and with what speed will it reach the bottom if
. How far from the bottom will the cylinder move and with what speed will it reach the bottom if
a)  =30o and
=30o and 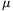 =0.2;
=0.2;
b)  =20o and
=20o and 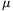 =0.4?
=0.4?
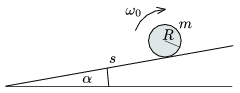
Data: s=2 m, R=0.2 m, 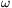 0=100 s-1.
0=100 s-1.
(5 pont)
P. 3992. A hemisphere of mass M and of radius R can slide on the horizontal tabletop without friction. A small object of mass m slides down from the top of the hemisphere without friction.
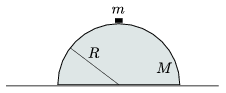
a) To what speed will the hemisphere be accelerated?
b) With what speed and where will the small object reach the table?
(5 pont)
Upload your solutions above.
