KöMaL Problems in Informatics, October 2007
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'I'Deadline expired on November 15, 2007. |
I. 166. By using a spreadsheet application, create a random but realistic map in a three-dimensional perspective view similar to the picture on the front/back cover of our Journal. The surface contour is generated from a diagram consisting of integers between 0 and 10 (representing altitudes) in a block of 40×40 cells of a worksheet. A button should appear below the data on this datasheet which, when pressed, regenerates all the data (that is the whole terrain). The actual view of the terrain should be visible on a diagram below the data and the button.
Your worksheet (i166.xls, i166.ods, ...) together with a short documentation of the solution (i166.txt, i166.pdf, ...) should be submitted containing also the name of the spreadsheet application and its version number.
(10 pont)
solution (in Hungarian), statistics
I. 167. We know that a very tiny - in fact, to us invisible - flea is jumping on certain integer coordinates of a ruler between 0 and 7 according to the following rule: in every second its next position will be the sum of its current and previous positions modulo 8. We want to catch the flea, but we can check only one position in every second.
Your task is to give a sequence of length of at most 30 so that if we check positions on the ruler in every second according to this sequence, we will surely catch the flea at the end. The shorter your sequence, the more points you may receive. An Excel sheet is available at www.komal.hu to check your sequences.
You can use any tools (e.g., write a program or use a spreadsheet) to complete the solution. Your sequence should be submitted (possibly using the downloadable compressed Excel sheet (bolha.zip) above) together with some remarks (i167.txt, i167.pdf, ...) commenting on your solution.
(10 pont)
solution (in Hungarian), statistics
I. 168. We set up a wireless network in a rectangular room by installing three WiFi antennas. We know that the strength of the signal is inversely proportional to the square of the distance from the antenna, further, every computer in the room receives the signal which is the strongest at that position. For simplicity we assume that the room can be covered by squares with side length of 1 m. The computers and antennas are in the interior of these squares. The distance of two squares is defined as the minimum number of squares connecting the original two. (Hence the distance of a square from itself is one.) The signal strength computed this way is rounded to the nearest integer.
Let us consider the following example. The size of the room is 4×3 square meters, and the positions of the antennas are at (4,3) with strength of 90, at (1,1) with strength of 70, and at (1,3) with strength of 60. The corresponding coverage diagram of the room is then the following:
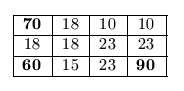
The signal strength within square (4,3) is 90, since the distance from the nearest antenna here is 1. Adjacent squares have signal strength of 23, since now the distance is 2, and is rounded to 23.
Write a program that creates a coverage diagram for a room of size of at most 25×25. The size of the room, the coordinates of the antennas and their strength are given as input to the program. The coverage diagram should be displayed on the standard output using a similar format as in the example (with values rounded to integers and each occupying 3 characters).
You should submit the source code of the program (i168.pas, i168.cpp, ...), a short documentation of your solution (i168.txt, i168.pdf, ...) and the name and version number of the compiler (e.g.,. Free Pascal 2.0, Borland C++ 3.1, ...).
(10 pont)
 |
Problems with sign 'S'Deadline expired on November 15, 2007. |
S. 29. Readers of our Journal might remember Problem I. 136. about the Sudoku game. The aim of this well-known puzzle is to fill in a 9×9 grid with digits between 1 and 9 so that each row, column and 3×3 subgrid contain only one instance of each digit.
Write a program that solves a partially completed Sudoku grid according to the following rules:
- if there is a unique solution, then the output should be the complete grid (that is, 9×9 digits, given in 9 rows),
- if the solution is not unique, then a possible solution should be displayed in 9 rows, while a warning ``Solution is not unique'' in the 10th row,
- if there is no solution, then simply display ``No solution''.
The name of the input text file is given as the first argument in the command line. This file contains 9 rows with given digits. Dots denote missing digits. The output should be written to the standard output.
You should submit the source code of the program (s29.pas, s29.cpp, ...), a short documentation of your solution (s29.txt, s29.pdf, ...) and the name and version number of the compiler (e.g., Free Pascal 2.0, Borland C++ 3.1, ...).
(10 pont)
$Var(Body)
Upload your solutions above
