KöMaL Problems in Informatics, November 2007
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'I'Deadline expired on December 17, 2007. |
I. 169. We are given N thin rods. We fix one end of the first rod and let it rotate around this hub with angular velocity of 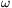 1. One end of the next rod is attached to the free end of the previous rod, and is rotating with relative angular velocity of
1. One end of the next rod is attached to the free end of the previous rod, and is rotating with relative angular velocity of  i (compared to the previous rod). This way we get a chain of connected rods. At the beginning, all rods are pointing to the same direction.
i (compared to the previous rod). This way we get a chain of connected rods. At the beginning, all rods are pointing to the same direction.
Your program should draw the path of the free end of the last rod. The input for your program should be the number of rods N (1 N
N 10) and 2N nonnegative integers: the length Li (1
10) and 2N nonnegative integers: the length Li (1 Li
Li 100) and relative angular velocity
100) and relative angular velocity  i of the ith rod.
i of the ith rod.
See the examples.
The source code of your program (i169.pas, i169.cpp, ...) together with a short documentation (i169.txt, i169.pdf, ...) should be submitted, also containing a short description of your solution and the developer environment to use.
(10 pont)
solution (in Hungarian), statistics
I. 170. Nervous John works as a system administrator for a company. One day he accidentally deleted a program used by his boss, Forgetful Fred. The purpose of that program was to put digital signatures at the end of e-mails: Fred chose a word (``signature'') depending on the content of the mail, wrote it at the end, then used the program to generate a ``code'' from the signature, and wrote the code also at the end of the mail. In order to make sure that a mail has been signed by Fred, he only had to enter the signature into his program and check if the generated code was the same.
Unfortunately, John could recover only 3 e-mails with the following signatures/codes:
Nemes/wiqiRd
kemence/igriqioh
TROMBITA/EXMFQSVXP
Your task is to help John and reconstruct Fred's program. The input should be a signature, then the code, as the output, should be written on the screen. The source code (i170.pas, i170.cpp, ...) should be submitted.
(10 pont)
solution (in Hungarian), statistics
I. 171. You should evaluate a school survey using a spreadsheet application. The data is found in the worksheet ``Skills''. The first rows of the sheet (with the exception of the first cells) contain a short (one-word) description of the skills surveyed. For example, cell B1 contains ``Speech'', C1 ``Writing'', D1 ``Counting'' and so on. Seven skills have been surveyed. Students in this test attended the same grade, and were from classes ``A'' to ``F''. There are at most 300 students. Beginning with the second row of the same worksheet, there are the class letters of each student and his or her results; so column A contains one of the following: Class A, Class B, ..., Class F, then the consecutive columns contain the results for each skill as an integer between 1 and 100, or 0 (or empty cell) if the student was not present when that skill was tested.
The worksheet ``Evaluation'' contains information on how to evaluate each skill and sort students into five groups. Suppose, for example, that ``Counting'' is divided into the following categories: Group I contains students with 1---24 points, Group II from 25 to 45 points, Group III from 46 to 58, Group IV from 59 to 80, while Group V from 81 to 100. Then, beginning with its first column, one of the first 7 rows of the sheet contain the values ``Counting'', ``24'', ``45'', ``58'', ``80'' and ``100''. Thus, the first column is the name of the skill, then the six other columns contain the largest possible values of each of the 5 groups. However, the order of the skills on worksheets ``Skill'' and ``Evaluation'' may be different.
You should make a third worksheet ``Results'' so that one can easily read off answers to the following questions:
the number of students that have been surveyed, from each class, or according to different skills, or altogether
how many students are there in the five groups of each skill, from each class or altogether
what will be the order of the classes if sorted according to each skill, or all skills together (``Class X'' precedes ``Class Y'', if Class X has more students in the group of the highest value (``Group V''), or, if this number of students is the same, then in the group just below it (``Group IV'') and so on).
You should submit the spreadsheet (i171.xls, i171.ods, ...) and a short documentation (i171.txt, i171.pdf, ...) containing a description of your solution, further, the name and version number of the spreadsheet application.
(10 pont)
 |
Problems with sign 'S'Deadline expired on December 17, 2007. |
S. 30. We would like to determine where puddles and pools are formed if the amount of precipitation is given. For simplicity, we consider only the cross-section of the given region, which is divided into horizontal line segments of fixed length with known relative altitudes. We can suppose that the distribution of precipitation is uniform.
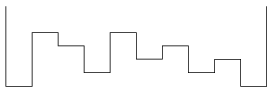
Water flows from higher areas to the neighbouring lower ones. If a segment has two lower neighbours, then the amount of water flowing down is equally divided between those neighbours. Water on the boundary segments can only flow inward.
Write your program to determine where water finally accumulates after the rain.
The input of your program is file s30.in. The first line of this file contains 2 integers separated by a space describing the amount of precipitation in millimeters and the number N of segments (). The second line contains N integers representing the height of each segment in millimeters relative to the lowest one.
The output of your program is s30.out, containing a single line with N digits separated by spaces. The ith digit is 1, if the ith segment contains water finally, otherwise 0.
The example corresponding to the above figure is the following:

(10 pont)
$Var(Body)
Upload your solutions above
