Competitions Portal

Problems in Mathematics, November 2007

Please read the rules of the competition.

Problems sign 'A'

Deadline expired.

A. 437. Let p>3 be a prime and

$1+\frac{1}{2}+\frac{1}{3}+\ldots+\frac{1}{p} = \frac{a}{b}.$

Prove that p⁴ divides ap-b.

(5 points)

A. 438. On the circumcircle of the equilateral triangle ABC, choose an arbitrary point P on arc AB. Mark the points Q and R on arc BC and the points S and T on arc CA for which AP=BQ=CR=CS=AT holds. Let lines BQ and PR meet at U and let lines AS and PT meet at V. Finally, let lines AU and BV meet at W. Show that each two of lines AU, BV and PW enclose an angle of 60^o.

(5 points)

Solution, statistics

A. 439. Prove that

$\frac{a_1^2}{1-a_1} + \frac{a_2^2}{a_1-a_2} + \frac{a_3^2}{a_2-a_3} + \ldots + \frac{a_n^2}{a_{n-1}-a_n} > \frac12(a_1+2a_2+3a_3+\ldots+na_n)-1$

whenever $1>a_1>a_2>\ldots>a_n>0$ .

(5 points)

Solution, statistics

Problems sign 'B'

Deadline expired.

B. 4032. 2007 natural numbers are written on the circumference of a circle. Is it possible that if the larger of each pair of two adjacent numbers is divided by the smaller one, the result is always a prime number?

(3 points)

Solution (in Hungarian)

B. 4033. All the participants in a dance course are married couples. Someone noticed that the difference between the heights of the two members of each couple is at most 10 cm. The dance instructor asks both the men and the women to stand in a line in increasing order of heights. Dancing couples are made by this rule: The tallest woman dances with the tallest man, and so on. Prove that the differences between the members of every dancing couple are also at most 10 cm.

(4 points)

Solution (in Hungarian)

B. 4034. The midpoint of one side of a triangle is F, and the points dividing another side into three equal parts are H₁ and H₂. The third side is divided into n equal parts by the points $N_1, N_2, \ldots, N_{n-1}$ . Consider all triangles FH_iN_j where i=1,2, $j=1,\ldots,n-1$ . Show that for any triangle selected out of these triangles there is exactly one other triangle that has the same area.

Suggested by T. Káspári, Paks

(3 points)

Solution (in Hungarian)

B. 4035. Solve the following equation: 2cos 5x+2cos 4x+2cos 3x+2cos 2x+2cos x+1=0.

(5 points)

Solution (in Hungarian)

B. 4036. The circles k₁ and k₂ touch each other on the outside at P. One of their common tangents not passing through P is e, which touches k₁ and k₂ at A and B, respectively. The line f is parallel to e, touches k₁ at C and intersects k₂ at D and E. Prove that the common chord of the circumcircles of the triangles ABC and ADE contains P.

(5 points)

Solution (in Hungarian)

B. 4037. Let f(n) denote the sum of the digits of the positive integer n in decimal notation. What may f(3a) be if f(a)=100 and f(124a)=700?

(4 points)

Solution (in Hungarian)

B. 4038. The reflections of an interior point P of triangle ABC about the midpoints of the sides BC, CA and AB are A', B' and C', respectively. Show that the lines AA', BB', CC' are concurrent.

(3 points)

Solution (in Hungarian)

B. 4039. Ann és Bill take turns writing digits of 0 or 1 from left to right next to each other. Ann starts. The game ends when each of them has written down exactly 2007 digits. The resulting sequence of zeros and ones is read as a number written in binary notation. Ann wins if the result is the sum of two perfect squares and Bill wins if it is not. Which of them has a winning strategy?

(4 points)

Solution (in Hungarian)

B. 4040. a, b, c are positive real numbers, and ab+bc+ca=1. Prove that

$\frac{1-a^2}{1+a^2}+\frac{1-b^2}{1+b^2}+\frac{1-c^2}{1+c^2}\le\frac{3}{2}.$

(5 points)

Solution (in Hungarian)

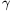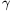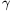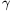B. 4041. The lengths of the medians of a triangle are a, b, c. Prove that for all positive numbers $\alpha$ , $\beta$ , $\gamma$ it is possible to construct a triangle with sides $\alpha$ a+ $\beta$ b+ $\gamma$ c, $\gamma$ a+ $\alpha$ b+ $\beta$ c, $\beta$ a+ $\gamma$ b+ $\alpha$ c.

(4 points)

Solution (in Hungarian)

Problems sign 'C'

Deadline expired.

C. 915. Which prime numbers can be expressed as a sum of two positive composite numbers?

(5 points)

Solution (in Hungarian)

C. 916. In 2006, the income of an insurance company increased by 25% and its expenses increased by 15% relative to the previous year. The profit ( $\hbox{income}-\hbox{expenses}$ ) of the company increased by 40%. What percentage of the income was taken by the expenses in 2006?

(5 points)

Solution (in Hungarian)

C. 917. Solve the following simultaneous equations:

x+2y+3z+4v=a,

y+2z+3v+4x=b,

z+2v+3x+4y=c,

v+2x+3y+4z=d,

where a, b, c, d are given real numbers.

(5 points)

Solution (in Hungarian)

C. 918. Connect the midpoints of the sides of a rectangle to the opposite faces. The eight lines obtained in this way form an octagon. What fraction of the whole area of the rectangle is the area of the octagon?

(5 points)

Solution (in Hungarian)

C. 919. A right-angled triangle is cut into a triangle and a quadrilateral by the perpendicular bisector of its hypotenuse. The ratio of the diagonals of the quadrilateral is $\big(1+\sqrt3\,\big):2\sqrt2$ . Find the acute angles of the right-angled triangle.

(5 points)

Solution (in Hungarian)

Problems sign 'K'

Deadline expired.

K. 139. Replace each circle between the numbers by the symbol of one of the basic operations so that the result is 100. (Note that brackets are not allowed.)

$1\ \circ \ 2\ \circ \ 3\ \circ \ 4\ \circ \ 5\ \circ \ 6\ \circ \ 7\ \circ \ 8\ \circ \ 9 = 100$

(6 points)

Solution (in Hungarian)

K. 140. If 73 hens lay 73 dozen eggs in 73 days and 37 hens eat 37 kg of wheat in 37 days, then how many kg of wheat are needed to produce a dozen eggs?

(6 points)

Solution (in Hungarian)

K. 141. The members of a board game club of students were asked this year again which of the four types of games they liked best. ``Civilisation building'' games lost their 12-vote lead they had last year and became second by a 6-vote difference. ``Train games'' came out first with 38% of all the votes. Games of ``extending your influence'' only got 14% of all votes and thus the fourth place, since ``merchant games'' received 4 more votes. How many members of the club voted for each type of game?

(6 points)

Solution (in Hungarian)

K. 142. In the Mathematical Olympiad of 2100, gold and silver medals will be made of pure gold and silver (and bronze medals will be made of bronze). The diameter of the silver medal will be 3 cm, with a thickness of 5 mm. (The shape of the medals will be as usual.) What will be the diameters of the gold and bronze medals if all the three kinds of medal have the same mass and thickness? (Densities: gold $19\;300~\rm kg/m^{3}$ , silver $10\;500~\rm kg/m^{3}$ , bronze 8930 kg/m³.)

(6 points)

Solution (in Hungarian)

K. 143. Tickets cost 1500 forints a piece in a cinema, but few people bought them for so much. When the managers decided to reduce the price, the average number of spectators per day increased by 50%, while the total daily income increased by 25%. What was the reduced price of a ticket?

(6 points)

Solution (in Hungarian)

K. 144. Consider the seven-digit numbers made out of the digits 1, 2, 3, 4, 5, 6, 7 by using each of them once. What is the sum of all such numbers?

(6 points)

Solution (in Hungarian)

Send your solutions to the following address:

or by e-mail to:

solutions@komal.hu

Our web pages are supported by:

ELTE