KöMaL Problems in Mathematics, February 2008
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on March 10, 2008. |
K. 157. Street lamps in a village are placed at equal intervals along the road. I observed that during 1 minute I passed as many lamp posts as 1/12 of my speed in km/h. Given that I was moving at a uniform speed and I started and finished counting when I was midway between two posts, calculate the separation between lamp posts.
(6 pont)
solution (in Hungarian), statistics
K. 158. A square garden is formed in a park out of four flowerbeds (as shown in the Figure). A single type of flowers are planted in each flowerbed, so that adjacent beds contain different types. (It is allowed to plant the same type of flower in opposite beds.) The flowers are selected out of three types: roses, lilies or gladioluses. In how many different ways can the garden be organized if orientation matters, too (that is, if it makes a difference which kind of flowers are planted in the north, south, east and west flowerbed)?
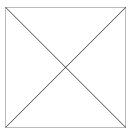
(6 pont)
solution (in Hungarian), statistics
K. 159. Jack and Jill start simultaneously at the bottom of the escalator. The escalator is moving uniformly upwards, and the children are also walking uniformly up the escalator without skipping any stair. Jill takes 40 seconds to get to the top, and in doing so she walks 40 steps. Jack takes 50 seconds and the number of his steps is 20. Then the escalator is stopped owing to technical problems and passengers need to walk up the stairs. How many steps will they take (without skipping any stair)?
(6 pont)
solution (in Hungarian), statistics
K. 160. Jack loves playing the following memory game: There are 18 kinds of picture cards, two copies of each. The 36 cards are shuffled and all layed on the table face down. The game consists of turns. In each turn, two cards are turned face up. If they are a pair of identical cards, they are removed from the table. If not, they are turned face down again. The game continues until he has removed all cards from the table. Since Jack has excellent memory, he can always remember the position of any card that he has seen. With this condition, is it possible for a game to consist of 17 turns? Of 18 turns? Of 35 turns? If so, give an example for a possible game. If not, explain why. (Assume that Jack is always trying to finish the game in the lowest number of turns, that is, he will not turn up cards again that he has already seen.)
(6 pont)
solution (in Hungarian), statistics
K. 161. Add all positive integers for which the quotient and remainder are equal if the number is divided by 2008. What is the result?
(6 pont)
solution (in Hungarian), statistics
K. 162. Side AB of rectangle ABCD is 2 units long and side AD is 3 units. The lengths of the line segments AC and CE are equal (see the Figure). What is the length of line segment BE?
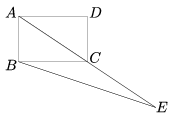
(6 pont)
 |
Problems with sign 'C'Deadline expired on March 17, 2008. |
C. 930. A game uses 11 red, 7 blue and 20 green counters. The bank returns two green counters for one red and one blue, two blue counters for one red and one green, and two red counters for one blue and one green. In making these trades, the player is trying to achieve that he has counters of a single colour. Which colour?
(5 pont)
solution (in Hungarian), statistics
C. 931. Find all positive integers, such that the result is 2007 if the sum of the digits is subtracted from them.
(5 pont)
solution (in Hungarian), statistics
C. 932. How many triangles of different shapes are there in which the measures of the angles in degrees are all integers?
(5 pont)
solution (in Hungarian), statistics
C. 933. ABC is a given triangle. Find that line passing through the vertex C where the perimeter of triangle ABD is greater than the perimeter of the triangle ABC for all points D of the line that are different from C.
Suggested by G. Holló, Budapest
(5 pont)
solution (in Hungarian), statistics
C. 934. Three rods of negligible thickness are fixed to each other in a common point at one end, in pairwise perpendicular positions. The lengths of the rods are 1, 2 and 3. The rigid structure is placed on the table with the free ends of the rods touching the table. Determine the height of the common endpoint above the plane of the table.
(5 pont)
 |
Problems with sign 'B'Deadline expired on March 17, 2008. |
B. 4062. Is it possible to draw a) 13, b) 14 circles on the plane, such that each of them is tangent to exactly three others?
(4 pont)
solution (in Hungarian), statistics
B. 4063. Al and Bill take turns choosing cards one by one from the deck of 81 SET cards (see the article on page http://galileo.stmarys-ca.edu/bdavis/set.pdf) and placing them on the table. When SET first appears on the table, the player placing the last card loses the game. If Al begins, which player has a winning strategy?
R. Deme-Farkas and P. Csikvári
(4 pont)
solution (in Hungarian), statistics
B. 4064. Given five lattice points on the coordinate plane, show that there is a pair among them, such that the midpoint of the line segment formed by them is also a lattice point.
(3 pont)
solution (in Hungarian), statistics
B. 4065. Let G be a simple graph in which the degree of every vertex is at least 2. Show that G has a vertex, such that every edge drawn from that vertex belongs to a circuit.
(3 pont)
solution (in Hungarian), statistics
B. 4066. Prove that if both midlines of a quadrilateral halve its area then the quadrilateral is a parallelogram.
(4 pont)
solution (in Hungarian), statistics
B. 4067. Erect a perpendicular to each of the sides AB, BC, CA of a triangle of perimeter k at the vertices A, B, C, respectively. Let K denote the perimeter of the new triangle obtained from the perpendiculars. Prove that , where
 ,
,  and
and 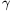 are the angles of the triangle ABC.
are the angles of the triangle ABC.
(3 pont)
solution (in Hungarian), statistics
B. 4068. Let A, B, C, a, b, c denote positive integers, a.b.c>1. Prove that there exists a positive integer n, such that A.an+B.bn+C.cn is a composite number.
(4 pont)
solution (in Hungarian), statistics
B. 4069. The lengths of the tangents drawn from the points A and B to a circle k are a and b, respectively. T is a point of the circle not collinear with A and B for which . Prove that the circle passing through the points A, B, T touches k.
(5 pont)
solution (in Hungarian), statistics
B. 4070. The positive integers a and b, written in decimal system, can be obtained from each other by rearranging their digits. Prove that
a) the sum of the digits of 2a equals that of 2b;
b) if both a and b are even, then the sum of the digits of equals that of
.
Kvant
(5 pont)
solution (in Hungarian), statistics
B. 4071. Prove that for every positive integer n, .
I. Blahota
(4 pont)
 |
Problems with sign 'A'Deadline expired on June 16, 2008. |
A. 446. The lengths of tangents drawn from the points A, B and C to a sphere s are a, b and c, respectively. T is a point on the sphere, not co-planar with A, B and C, such that .
Prove that the sphere passing through the points A, B, C, T touches s.
(5 pont)
A. 447. Prove that the inequality is true for all real numbers a1,a2,...,an.
(5 pont)
A. 448. The numbers 1,2,...,N are colored with 3 colors such that each color is used at most times. Let A be set of all (ordered) 4-tuples (x,y,z,w), consisting of such numbers, such that
and x, y, z, w have the same color. Similarly, let B be the set of all (ordered) 4-tuples (x,y,z,w) such that
, the numbers x, y have the same color, z and w have the same color, but these two colors are distinct. Prove that |A|
 |B|.
|B|.
(5 pont)
Upload your solutions above.
