KöMaL Problems in Mathematics, April 2008
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'C'Deadline expired on May 15, 2008. |
C. 940. Prove if n is a positive integer then 24n-1 or 24n+1 is divisible by 17.
(5 pont)
solution (in Hungarian), statistics
C. 941. There are two lamps on the ceiling of a rectangular classroom of length 10 m. They emit conical light beam of apex angles of 90o. One is situated in the middle of the ceiling, and illuminates a circle of diameter 6 m on the floor. The lampshade of the other lamp is turned so that the illuminated region on the floor is long enough to draw a line segment of length 10 m on it in the direction parallel to the length of the room, but no light falls on the walls at the ends of the room. Find the distance between the two lamps.
(5 pont)
solution (in Hungarian), statistics
C. 942. In an arithmetic progression of common difference d, a1=1 and an=81. In a geometric progression of common ratio q, b1=1 and bn=81. Given that , find all such sequences.
(5 pont)
solution (in Hungarian), statistics
C. 943. The area of a sector of a circle is 100. what is the radius if the perimeter is a minimum?
(5 pont)
solution (in Hungarian), statistics
C. 944. Rick, Dan and Alan play table tennis with two players at one side of the table and the third one at the other side. Dan and Alan playing together beat Rick three times as often as Rick beats them, Dan wins the game against Rick and Alan as often as he loses it, and Alan wins the game against Rick and Dan twice as often as he loses it. Last time they played six games during the afternoon, two in each arrangement of players. What is the probability that Rick won at least once?
(5 pont)
 |
Problems with sign 'B'Deadline expired on May 15, 2008. |
B. 4082. The diagram shows a plane figure that cannot cover a unit semicircle but two congruent copies of the figure can cover a unit circle. Is there a convex figure that has the same property?
Kvant
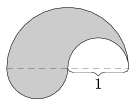
(4 pont)
solution (in Hungarian), statistics
B. 4083. Each of the digits 0 to 9 is written in 10 fields of a 10×10 table. Is it possible that every row and every column has at most 4 different digits in it?
Kvant
(4 pont)
solution (in Hungarian), statistics
B. 4084. Find all sequences (an) of positive integers, such that (ai,aj)=(i,j) for all i j.
j.
(3 pont)
solution (in Hungarian), statistics
B. 4085. Prove that if a symmetrical trapezium has an inscribed circle then its height is the geometric mean of the bases.
(3 pont)
solution (in Hungarian), statistics
B. 4086. Four points are selected at random on a sphere, independently of each other. What is the probability that the resulting tetrahedron contains the center of the sphere?
(5 pont)
solution (in Hungarian), statistics
B. 4087. Prove that if the lengths of the sides of a triangle are 2, 3 and 4 then it has angles  and
and  , such that 2
, such that 2 +3
+3 =180o.
=180o.
Suggested by Z. Varga, Siófok
(3 pont)
solution (in Hungarian), statistics
B. 4088. P is an interior point of side B1B2 of an acute-angled triangle AB1B2. Let Q denote the reflection of P about point A. Let Di denote the perpendicular projection of P onto the line segment ABi, and let Fi be the midpoint of the line segment DiBi. Prove that if QD1 is perpendicular to PF1, then QD2 is perpendicular to PF2.
Suggested by J. Bodnár, Budapest
(5 pont)
solution (in Hungarian), statistics
B. 4089. Solve the equation x4-7x3+13x2-7x+1=0.
(4 pont)
solution (in Hungarian), statistics
B. 4090. The angle bisector f drawn from vertex A of an acute-angled triangle ABC intersects side BC at D and the circumscribed circle at E. The altitude drawn from C intersects f at M and the circumscribed circle at Q. The altitude drawn from B intersects f at N and the circumscribed circle at P. Prove that
(4 pont)
solution (in Hungarian), statistics
B. 4091. Prove that
for arbitrary positive integers m, t.
(5 pont)
 |
Problems with sign 'A'Deadline expired on May 15, 2008. |
A. 452. A simple graph on 2n points has n2+1 edges. Prove that the edges form at least n triangles.
(5 pont)
A. 453. n points are selected at random on a sphere, independently of each other. What is the probability that the convex hull of the selected points contains the center of the sphere?
(5 pont)
A. 454. Is there any polynomial p having degree at least 1 over the reals that satisfies p2(x)-1=p(x2+1) for all real numbers x?
(5 pont)
Upload your solutions above.
