KöMaL Problems in Informatics, October 2008
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'I'Deadline expired on November 17, 2008. |
I. 193. Teddy found an old tape recorder together with several cassettes and he wanted to copy these sound recordings onto his computer. One of the cassettes however contained a strange noise, although Teddy was sure that this, too, could be made intelligible with a suitable transformation. To this end, he tried to use the freely downloadable program Audacity, but could not manage to decode the tape. You will get 10 points, if you can restore the content of file I193.mp3, that is, make it as clear and intelligible as possible.
You should submit the transformed sound file (i193.mp3) together with a short documentation (i193.txt, i193.pdf, ...) describing your solution.
(10 pont)
solution (in Hungarian), statistics
I. 194. There are various types of barcodes, but in commerce EAN-13 (EAN = European Article Number) is most commonly used. This barcode represents a 13-digit number in the following way.
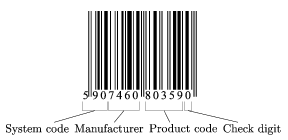
The above parts may consist of various numbers of digits. The System code refers to a country or the type of the product. For example:
|
When a new product is released, the manufacturer can obtain a new EAN-13 code from a central database.
The last digit of an EAN-13 code is the Check digit, which gives some protection against a random misprint or improper reading of the barcode. To form this checksum, we compute a weighted sum of the first 12 digits as follows: digits at odd positions are multiplied by 1, while digits at even positions are multiplied by 3, then these products are added. This sum is rounded up to the nearest whole ten number. The 13th digit is defined by the increment made in the last step.
In the above example: 5.1+9.3+0.1+7.3+4.1+6.3+0.1+8.3+0.1+3.3+5.1+9.3=140. Since 140 is already divisible by 10, no rounding up is necessary, so the increment, and hence the Check digit should be 0. This shows that the EAN-13 barcode in the example is valid.
The layout of the barcode is described below.
- Digits are encoded by black and white areas. Scanners read these.
- The first separated digit on the left determines the method of encoding. No bars correspond to it, so it is encoded differently.
- The rest of the code contains two groups of digits. In front of, behind and between the groups there are thin double lines.
- Each digit is represented by 2 lines with varying thickness, occupying 7 units of width. There can be 3 different encodings within a barcode. Let us denote these by A, B or C. The 2 lines can be converted into digits according to the table (``Szám'' means ``Digit''), where black colour is 1 and white is 0.
|
- The first group of digits (that is, digits from position 2 to position 7) are encoded either by A or B, while the second group (consisting of the last 6 digits) is encoded by scheme C.
- The first digit of the EAN-13 barcode determines the type of encodings of the six digits in the first group according to the table (``Első számjegy'' means ``First digit'').
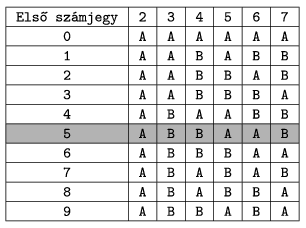
The structure of the barcode in the example (a marmalade jar from Poland): The first digit is 5, which is not encoded by lines, but determines the encoding type of the first group according to the highlighted row of the table above.
|
Putting all these together we obtain the barcode.

Using a spreadsheet application, determine whether the EAN-13 barcode in cell A1 is valid, using the Check digit: you should write either ``valid'' or ``invalid'' into cell B1. Then you should convert the given sequence of digits into a sequence of lines encoded by 0s and 1s in cells A2:A16 (as in the Thickness column of the example above).
You should not use macros or program modules, only formulae and built-in functions. Intermediate computations should be visible, so do not hide any of them. Auxiliary tables for the conversion can be placed on separate sheets.
Your worksheet (i194.xls, i194.ods, ...) together with a short documentation (i194.txt, i194.pdf, ...) should be submitted, also containing a brief description of your solution and the name and version number of the spreadsheet application used.
(10 pont)
solution (in Hungarian), statistics
I. 195. When using a satellite navigation system with touchscreen, it is enough to enter only the first few characters of the name of the destination, and the computer automatically displays the next optional characters. A character is optional, if there is (at least one) destination in the database whose name begins with the string entered by the user so far together with the optional character. When typing a character, the computer also gives the number of matches, that is, the number of destinations whose name begins with the characters entered so far. This number is displayed next to the input field.
Write a program that simulates such a satellite navigation system. The input file (given as the first command line argument to your program) contains a list of possible destinations. You can use the sample file telepules.txt for your solution. Your program should use the standard output. The output after entering a character should contain the list of optional characters and the number of matches. It should be possible for the user to enter only optional characters. Your program should stop if ESC is pressed.
Lowercase and uppercase letters are not distinguished, and accents should also be ignored, so, for example, Ó, ö, Ő and o are all displayed and treated as o.
Example: ÁBRA
The source code of your program (i195.pas, i195.cpp, ...) together with a short documentation (i195.txt, i195.pdf, ...) should be submitted, also containing a brief description of your solution and the name of the developer environment to use for compiling.
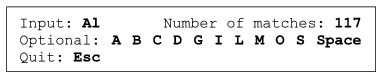
(10 pont)
 |
Problems with sign 'S'Deadline expired on November 17, 2008. |
S. 38. Web browsers create a document tree, when they display HTML pages. The root of the tree is a <HTML> element, and every other element is its descendant. The following example illustrates a HTML source and the corresponding document tree.

Write a program to create a document tree from a valid HTML 4.01 Strict DTD version page (that is, the page does not contain invalid formats and frames). Valid HTML elements are found at http://www.w3.org/TR/html401/index/elements.html
(only without marks D and L, altogether 80 elements). The first command line argument of your program is the name of the source file to be read, while the second command line argument is the name of the output text file containing the document tree in the above format.
The source code of your program (s38.pas, s38.cpp, ...) together with a short documentation (s38.txt, s38.pdf, ...) should be submitted, also containing a brief description of your solution and the name of the developer environment to use for compiling.
(10 pont)
$Var(Body)
Upload your solutions above
