KöMaL Problems in Mathematics, December 2008
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on January 10, 2009. |
K. 187. Fill in the blank cells of the Figure, so that the sum of the numbers in the three hexagons meeting at a vertex is always the same.
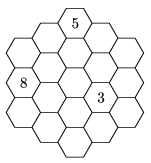
(6 pont)
solution (in Hungarian), statistics
K. 188. The base AB of an isosceles triangle ABC is extended beyond vertex B by the length of the leg. The endpoint obtained is C1. A perpendicular is erected onto the base AB at vertex A. C2 is the point on the perpendicular that lies in the same half plane as vertex C, at a distance from A that equals the length of the leg. Given that the points C1, C and C2 are collinear, find the angles of triangle ABC.
(6 pont)
solution (in Hungarian), statistics
K. 189. In a mathematics lesson, the teacher gave the students five kinds of problems to practise. There were three problems of each kind. Students got 1 mark for solving a single problem of a kind, 4 marks per problem if they solved two of the same kind, and 9 marks per problem if they solved all three of a kind. The students worked on the problems and received marks in teams. At the end of the lesson, every team had a different number of marks, but all their numbers of marks were found to be divisible by 3. What was the maximum possible number of teams?
(6 pont)
solution (in Hungarian), statistics
K. 190. In a vote, 55% of the boys and 5% of the girls voted ``Yes''. Thus the majority voted ``Yes''. How many boys may have voted ``No'' at least?
(6 pont)
solution (in Hungarian), statistics
K. 191. Two kinds of windscreen wiper are investigated. Each of them has a 31-cm blade attached to an also 31-cm arm at the middle. The arm rotates through a 90o angle when the wiper is in operation. One kind of wiper is rigid, the blade encloses 45o with the lower edge of the windscreen and points in the direction of the arm throughout the wiping process. In the other wiper, the blade is attached to the arm by a hinge, and it remains perpendicular to the lower edge of the windscreen all the way long. Which type of wiper sweeps through a larger area?
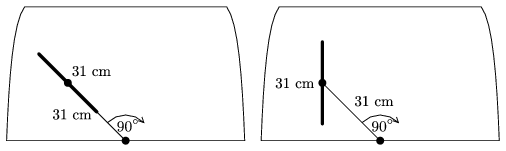
(6 pont)
solution (in Hungarian), statistics
K. 192. Ann, Beth and Cathy all filled out the same test of six true-or-false questions. Ann's answers (in this order) were F, F, T, T, T, T; Beth's answers were (in this order) T, F, F, T, T, T, and Cathy's answers (in this order) were T, T, F, F, T, T. Ann only got two answers wrong and Beth got only two of them right. How many correct answers may Cathy have got?
(6 pont)
 |
Problems with sign 'C'Deadline expired on January 15, 2009. |
C. 965. The pattern in the Figures consists of black, white and grey squares. Which Figure in the sequence will contain 2112 grey squares?
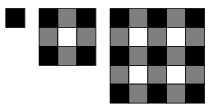
(5 pont)
solution (in Hungarian), statistics
C. 966. Hungarian licence plates of vehicles contain (three letters and) three digits. The digits do not need to be different. Someone observed that on the average, the licence plates of nearly 3 vehicles out of 10 contain identical digits. Is he right?
(5 pont)
solution (in Hungarian), statistics
C. 967. Solve the following simultaneous equations:
3x2-xy=1,
9xy+y2=22.
(5 pont)
solution (in Hungarian), statistics
C. 968. As shown, the square ABCD is divided, with lines parallel to its sides, into the squares NPLD and KBMP, and two congruent rectangles. Let P denote the intersection of KL and MN, and let Q be the intersection of BN and DK. Show that the points C, P and Q are collinear.
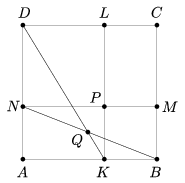
(5 pont)
solution (in Hungarian), statistics
C. 969. The arms of a pair of compasses need to be opened through an angle twice as wide to draw a circle of radius 6.5 cm as for a circle of radius 3.3. How long are the arms of the compasses?
(5 pont)
 |
Problems with sign 'B'Deadline expired on January 15, 2009. |
B. 4132. Annie and Bonnie are playing the following game on a 2008×2008 chessboard: Annie selects a few fields of the board but does not tell Bonnie which. Then she writes in each field the number of selected fields that it is connected to by an edge or vertex. Is that enough information for Bonnie to tell which fields were selected? What is the answer if they play on a 2009×2009 board?
Suggested by D. Nagy
(5 pont)
solution (in Hungarian), statistics
B. 4133. P and Q are points on the sides BC and CD of a rectangle ABCD, such that the triangle APQ is equilateral. Prove that tAQD+tABP=tPCQ.
(3 pont)
solution (in Hungarian), statistics
B. 4134. Let denote the number of three term arithmetic progressions that can be selected from the terms of a sequence a1<a2<...<ak. Prove that
.
(4 pont)
solution (in Hungarian), statistics
B. 4135. M is a point in the interior of a square ABCD, such that DCM =MAC
=MAC =25o. Find the measure of the angle ABM.
=25o. Find the measure of the angle ABM.
(4 pont)
solution (in Hungarian), statistics
B. 4136. Given a convex quadrilateral, construct a rhombus with vertices lying on the sides of the quadrilateral, and sides parallel to the diagonals of the quadrilateral.
(3 pont)
solution (in Hungarian), statistics
B. 4137. Let n be a positive integer. Prove that is divisible by 2n-1.
(5 pont)
solution (in Hungarian), statistics
B. 4138. Solve the following equation: .
(4 pont)
solution (in Hungarian), statistics
B. 4139. Two altitudes of an acute-angled triangle ABC are BE and CF. Line EF intersects the circumscribed circle at P and Q. Prove that AP=AQ.
(4 pont)
solution (in Hungarian), statistics
B. 4140. E is the midpoint of the arc BC on the circumscribed circle of a cyclic quadrilateral ABCD. The midpoint of arc DA is F. Let P and Q be the centres of the inscribed circles of triangles ABC and ABD, respectively. Show that PQ is parallel to EF.
(4 pont)
solution (in Hungarian), statistics
B. 4141. Prove that (a2+2)(b2+2)(c2+2) 3(a+b+c)2 is true for all real numbers a, b, c.
3(a+b+c)2 is true for all real numbers a, b, c.
(5 pont)
 |
Problems with sign 'A'Deadline expired on February 16, 2009. |
A. 467. Let ABCD be a circumscribed trapezoid such that the lines AD and BC intersect at point R. Denote by I the incenter of the trapezoid, and let the incircle touch the sides AB and CD at points P and Q, respectively. Let the line through P, which is perpendicular to PR, meet the lines angle bisector AI and BI at points A1 and B1, respectively. Similarly, let the line through Q, perpendicular to QR, meet CI and DI at C1 and D1, respectively. Show that A1D1=B1C1.
Proposed by: Géza Bohner, Budapest
(5 pont)
A. 468. We are given two triangles. Their side lengths are a,b,c and A,B,C respectively, the areas are t and T, respectively. Prove that -a2A2+a2B2+a2C2+b2A2-b2B2+b2C2+c2A2+c2B2-c2C2 16tT.
16tT.
(5 pont)
A. 469. Let 0 k
k n and m
n and m 2 be integers. Consider the k-element subsets of
2 be integers. Consider the k-element subsets of ; in every such subset, compute the residue of the sum of elements, modulo m. Prove that if the m residues are distributed uniformly - i.e. every residue occurs exactly
times - then n
 m.
m.
(5 pont)
Upload your solutions above.
