KöMaL Problems in Informatics, January 2009
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'I'Deadline expired on February 16, 2009. |
I. 202. We are given some heaps of stones. In every step, we remove one stone from each heap and form a new heap out of these stones. The order of heaps is irrelevant.

The number of steps can be arbitrary. Since the number of stones is finite, sooner or later the distribution of stones in heaps becomes cyclic.
Write your program to compute the number of step in which repetition begins and determine the cycle length. The command line argument of your program is the name of the input file. The input file contains the initial distribution of stones in heaps: the first line of the input file contains the number of heaps N (being an integer with 1 N
N 25), the following N lines then contain the number of stones in the corresponding heaps. (The total number of stones, however, is no more than 50.)
25), the following N lines then contain the number of stones in the corresponding heaps. (The total number of stones, however, is no more than 50.)
In the example (``Példa''), the input is ``Bemenet'', and the output is ``Kimenet''.

The output of your program on the screen is two positive integers: the first gives the number of step in which a new cycle starts, while the second describes the length of a cycle.
The source code of your program (i202.pas, i202.cpp,...) together with a short documentation (i202.txt, i202.pdf,...) should be submitted, also containing a brief description of your solution and the name of the developer environment to use for compiling.
(10 pont)
solution (in Hungarian), statistics
I. 203. Suppose that a monkey is hitting letters randomly on a typewriter keyboard. If we wait long enough, then those random letters might produce meaningful words, even the complete works of William Shakespeare. The aim of the following experiment is to examine whether monkeys can produce a given text (being at most 3 characters long).
Description of the experiment. Take a monkey and a keyboard containing only the capital letters of the English alphabet. Choose a string, for example OR. In each experiment, wait for 50000 keystrokes, then determine the first position after which the chosen word completely appeared. (For example, if the monkey typed GJFORSFFX, then OR appeared after the 5th keystroke.) Save this value. (If the monkey did not type the given string, set that counter to 60000.)
Your task is to devise a suitable model to simulate the above experiment in a spreadsheet application. You can assume that the monkey hits each letter with equal probability. Experiment with the words FA, BOT, ORR (meaning TREE, STICK and NOSE in English), and with XP, PDF, PPT and MMM (which would be harder for a monkey to understand). However, your solution should be able to handle other words as well. Results of these experiments should be stored in the sheet ``measurements''. (These numbers are read off and entered by you.) No other data can be present on this sheet.

The translation of the text in cell A1 in the example is ``The actual string to be examined'', while cell A3 says ``String MMM in cell A2 appears after the 17719th keystroke on the average'', finally, the Hungarian word ``kísérlet'' is experiment. (These figures are only for illustration.)
The worksheet ``monkey'' should contain the characters typed by the monkey. (You can use an arbitrary format to store characters, but try to choose a layout that helps data processing.) Auxiliary computations (if necessary) can be stored in sheet ``aux''. The more experiments you make the better.
The compressed file i203.zip containing file i203.xls (or i203.ods) should be submitted together with a text file (i203.txt, i203.pdf, ...) specifying the version numbers of the programs applied. The text file should also contain your conjecture about the following question: which string of the form XYZ, XYX, XXY and XXX is the most probable to appear first and last in the monkey's text?
(10 pont)
I. 204. As we have seen in Problem I. 201. in our last Issue, the Cardan grille can be used to encode messages. Write a program that encodes a given text using a given grille, that is, produces a suitable arrangement of letters of the text according to the grille.
The structure of the grille in its initial position is read from a text file being the first command line argument of your program. If the size of the grille is N×N, then this file has N lines: each line consists of ``o'' or ``.'' characters. The ``o'' symbol represents a ``hole'': letters under these squares are visible. The original text is read from a text file specified by the second command line argument. This file (having one or more lines) can contain lowercase and uppercase letters of the Hungarian alphabet, further space characters and the usual punctuation marks. The output of your program should be a text file given in the third command line argument. This file should contain blocks of N×N letters, separated by empty lines.
Encoding starts from the beginning of the text, and successively creates blocks of N×N letters. These blocks can contain letters only from the original text, but converted into uppercase characters. Spaces, newline characters and other punctuation marks should not be included. Note that the encrypted text could be decoded easily if the last block of letters is incomplete (due to the fact that the original text has ended). To avoid this problem, you should copy the appropriate number of letters from the beginning of the text and attach these to the end of the text so that the last block of letters becomes complete.
In the example, ``Első fájl (a rács)'' means ``First file (grille)'', ``Második fájl (a szöveg)'' means ``Second file (original text)'', while ``Harmadik fájl (a titkos)'' is ``Third file (encoded)''.

The source code of your program (i204.pas, i204.cpp, ...) together with a short documentation (i204.txt, i204.pdf, ...) should be submitted, also containing a brief description of your solution and the name of the developer environment to use for compiling.
(10 pont)
 |
Problems with sign 'S'Deadline expired on February 16, 2009. |
S. 41. Problem I. 188. in our 2008 May Issue dealt with displaying line fractals, also known as L-systems, by a vector-graphics editor. Your program now should realize a simplified L-system.
The following axioms and rules should be available in your program:

The input of your program is an axiom (``Axióma'' in the example), a rule (``Szabályok''), the number of recursions (``Szint''), the length of movements (``Lépéshossz'') and the turning angle (``Szög'').
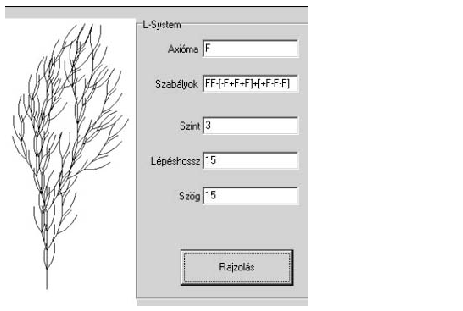
The axiom and rule can consist only of the given symbols. The input may be either textual or graphical, depending on the programming environment. The input can be assumed to be syntactically correct, so no further checking is needed.
The source code of your program (s41.pas, s41.cpp, ...) together with a short documentation (s41.txt, s41.pdf, ...) should be submitted, also containing a brief description of your solution and the name of the developer environment to use for compiling.
(10 pont)
$Var(Body)
Upload your solutions above
