KöMaL Problems in Mathematics, January 2009
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on February 10, 2009. |
K. 193. Four girls and four boys went dancing together. The first dance was a waltz. Each boy asked a girl to dance (each girl was only asked by one boy). The next dance was a tango. This time, it was the girls who asked the boys to dance. Each girl asked a boy (and each boy was asked by only one girl). There was no couple that danced both dances together. Given the following information, find out who danced each dance with whom.
a) Charles waltzed with the girl who danced tango with Daniel.
b) Andrew asked that girl to waltz who danced tango with the boy who waltzed with Emily.
c) Bernard waltzed with the girl who danced tango with Mary's waltz partner.
d) Gillian did not dance tango with Bernard.
e) Helen danced tango with a boy who did not waltz with Gillian.
After the two dances, when the dance instructor asked everyone to stand behind the back of the partner whom he or she asked to dance, the result was one big circle of people.
(6 pont)
solution (in Hungarian), statistics
K. 194. The decimal point was shifted one place to the left in a number, and the resulting number was added to of the original number. The result was 1406.3. What was the original number?
(6 pont)
solution (in Hungarian), statistics
K. 195. The isosceles triangle ABC has a right angle at A; the length of its legs is AB=AC=4 cm. The circles with centers at B and C of radius 4 cm intersect the hypotenuse at D and E, respectively. What is the area of the shaded domain? (See the Figure.)
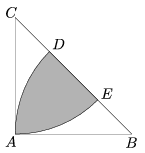
(6 pont)
solution (in Hungarian), statistics
K. 196. In a kite, there is a 90o angle opposite the 60o angle. It is symmetrical to its diagonal of length 10 cm. Find its perimeter.
(6 pont)
solution (in Hungarian), statistics
K. 197. Solve the equation x.|3-|x+5||=x.
(6 pont)
solution (in Hungarian), statistics
K. 198. The inhabitants of a certain planet use not four but five basic arithmetic operations. The operations of addition, multiplication, subtraction and division are the same as ours, but they also have a special operation denoted by the operation sign @. We do not know exactly how this operation works, but we have found out that the following properties are valid for all x and y:
(a) ,
(b) ,
(c) .
What is the value of on the planet in question?
(6 pont)
 |
Problems with sign 'C'Deadline expired on February 16, 2009. |
C. 970. Rose, Ivy and Violet decided to solve all problems in their book of mathematics problems. Rose solves a problems, Ivy solves b problems and Violet solves c problems a day. (Each problem is only solved by one of the girls.) If Rose solved 11 times as many problems a day, Ivy solved 7 times as many and Violet solved 9 times as many, they would finish the job in 5 days. If Rose solved 4 times as many, Ivy solved 2 times as many and Violet solved 3 times as many problems a day, they would take 16 days. How many days does it take them to get done with the solutions?
(5 pont)
solution (in Hungarian), statistics
C. 971. Is there a plane figure different from the unit square that has an area of 1 and a perimeter of 4?
(5 pont)
solution (in Hungarian), statistics
C. 972. There are 10 mail boxes next to the gate of a building. A man distributing flyers walks by and puts flyers in 5 boxes. Later another one walks by and also puts flyers in 5 boxes. What is the probability that there are fliers in at least 8 boxes?
(5 pont)
solution (in Hungarian), statistics
C. 973. Solve the equation: 1+cos 3x=2cos 2x.
(5 pont)
solution (in Hungarian), statistics
C. 974. ABCD is a cyclic trapezium. Diagonal BD is extended beyond vertex D by the length of the leg and the point L is obtained. K is the point on diagonal AC whose distance from C is equal to the leg. Prove that the areas of the rectangles formed by the line segments AB and CD and the line segments AK and BL are equal.
(5 pont)
 |
Problems with sign 'B'Deadline expired on February 16, 2009. |
B. 4142. A rectangular puzzle that says ``850 pieces'' actually consists of 851 pieces. Each piece is identical to one of the 5 samples shown in the diagram. How many pieces of type (E) are there in the puzzle?
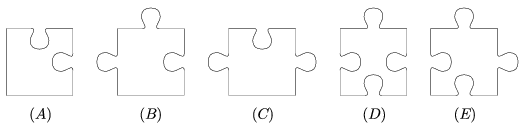
(4 pont)
solution (in Hungarian), statistics
B. 4143. Two adjacent vertices of a square lie on a unit circle. What are the smallest and largest possible distances of the other two vertices from the centre of the circle?
(4 pont)
solution (in Hungarian), statistics
B. 4144. Prove the following inequality: 2(x4+x2y2+y4) 3xy(x2+y2).
3xy(x2+y2).
(3 pont)
solution (in Hungarian), statistics
B. 4145. The longer base of a symmetrical trapezium ABCD is at most twice as long as the shorter base. P is a point in the interior of the trapezium. Prove that there exists a quadrilateral whose vertices lie on the sides of the trapezium and whose sides are of lengths AP, BP, CP and DP in some order.
(5 pont)
solution (in Hungarian), statistics
B. 4146. Show that the equation 5x2+3y2=1 has no solutions in the set of rational numbers.
(4 pont)
solution (in Hungarian), statistics
B. 4147. Prove that any right angled triangle can be extended to a rectangle by attaching to its sides three right angled triangles which are similar to each other.
(3 pont)
solution (in Hungarian), statistics
B. 4148. Solve the following system of equations:
x3y+xy3=10,
x4+y4=17.
(4 pont)
solution (in Hungarian), statistics
B. 4149. The orthogonal projections of a point onto the lines of the altitudes drawn from vertices A, B, C of a triangle are denoted by A1, B1, C1, respectively. Prove that there is exactly one point in the plane of the triangle for which the line segments AA1, BB1, CC1 are equal, and then the length of these line segments is equal to the diameter of the inscribed circle of triangle ABC.
Based on a problem in Kvant
(5 pont)
solution (in Hungarian), statistics
B. 4150. Two different digits of a number of at least 100 digits and not divisible by ten are interchanged, the resulting number has the same prime factors as the original number. Show an example for such a number.
(5 pont)
solution (in Hungarian), statistics
B. 4151. Let  =
=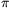 /14. Evaluate sin
/14. Evaluate sin  .sin 3
.sin 3 .sin 5
.sin 5 .
.
(4 pont)
 |
Problems with sign 'A'Deadline expired on February 16, 2009. |
A. 470. In the triangle ABC, denote by A1, B1, and C1 the feet of altitudes. Let P be the perpendicular foot C1 on line A1B1, and let Q be that point of line A1B1 for which AQ=BQ. Show that  PAQ=
PAQ= PBQ=
PBQ= PC1C.
PC1C.
(5 pont)
solution (in Hungarian), statistics
A. 471. Prove that if each vertex of a simple graph is of degree at least 3 then the graph contains a cycle with length not divisible by 3.
Russian competition problem
(5 pont)
A. 472. Call a finite sequence (p1(x),...,pk(x)) of polynomials with integer coefficients Euclidean if there exist polynomials with integer coefficients such that d(x)=q1(x)p1(x)+...+qk(x)pk(x) is a common divisor of p1(x),...,pk(x), i.e. there are polynomials
with integer coefficients for which pi(x)=ri(x)d(x) for every 1
 i
i k. Prove that whenever
k. Prove that whenever are polynomials with integer coefficients and every two of them form a Euclidean pair, then the sequence
is Euclidean as well.
(5 pont)
Upload your solutions above.
