KöMaL Problems in Mathematics, February 2009
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on March 10, 2009. |
K. 199. Dixie puts five-digit numbers in order, according to the following rule: First he arranges them in decreasing order of the last digit. If the last digit is the same in two numbers, the one with the smaller first digit will precede the other. If their first digits are also the same, they will be listed in decreasing order of the product of the middle three digits. (Dixie only deals with numbers whose order can be decided by this rule.) Dixie wrote six numbers on a sheet of paper. The numbers were ordered according to the rule above, but some digits got blurred. (The blurred digits are replaced by letters here.) It reads: 42348, A8318, 56B48, 8653C, 46585, D8655. Considering all possibilities, we try to guess the six numbers. (Our guess is one possible value for each number.) What is the probability that we will get all Dixie's numbers right?
(6 pont)
solution (in Hungarian), statistics
K. 200. There are 64 participants in a tennis tournament. Everyone plays games against the others. Any player who has lost three games will be eliminated. The participant who stays in alone at the end will win the competition. What are the minimum and maximum numbers of games played altogether in this competition?
(6 pont)
solution (in Hungarian), statistics
K. 201. In how many different ways is it possible to read the number 2009 from the figure below if successive fields must have an edge in common?
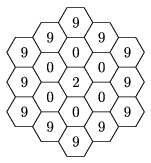
(6 pont)
solution (in Hungarian), statistics
K. 202. The number 99 999 989 999 is multiplied by itself. Without a calculator, determine the number of nines in the result.
(6 pont)
solution (in Hungarian), statistics
K. 203. Given that for all x
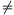 0, find the value f(2) of the function.
0, find the value f(2) of the function.
(6 pont)
solution (in Hungarian), statistics
K. 204. Consider the figure. What is the ratio of the area shaded to the area not shaded? (The curves bounding the figure are semicircles, and the points marked on the diameter divide it into three equal parts.)
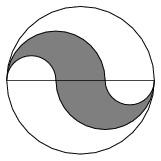
(6 pont)
 |
Problems with sign 'C'Deadline expired on March 16, 2009. |
C. 975. In triangle ABC, the altitude drawn from vertex C intersects side AB at T. Right-angled triangles CAD and CBE are drawn on sides AC and BC on the outside, such that the right angles are at A and B. Given that AD=TB and BE=TA, prove that  CDE=
CDE= CED.
CED.
(5 pont)
solution (in Hungarian), statistics
C. 976. The sum of three positive numbers is multiplied by the sum of their reciprocals. Find the smallest possible interval where the product may lie.
(5 pont)
solution (in Hungarian), statistics
C. 977. An entrepreneur has taken out a subsidized loan for 12 million forints (HUF, Hungarian currency) at a fixed annual interest rate of 8%. How much will he owe in 10 years if he pays back the loan in annual instalments of 1.2 million forints?
(5 pont)
solution (in Hungarian), statistics
C. 978. A café has tables for two. At the moment, there are six customers sitting at three tables. Three of them are having coffee and three are having tea. What is the probability that there is a table where both customers are having tea?
(5 pont)
solution (in Hungarian), statistics
C. 979. We have a red bouncy ball with thirty round white spots on it. (The spots form spherical caps.) The perimeter of the great circle of the ball is 54 cm, and the perimeter of the spots is 11 cm. What percentage of the surface area of the ball is covered by the spots?
(5 pont)
 |
Problems with sign 'B'Deadline expired on March 16, 2009. |
B. 4152. Given n different subsets of the set of numbers 1,2,3,...,n, prove that there exists a number, such that if it is left out of each subset, the remaining subsets will still be different.
(4 pont)
solution (in Hungarian), statistics
B. 4153. The centre of the circumscribed circle of triangle ABC is O, and its orthocentre is M. Mark the points E and F on the lines of sides AC and AB, respectively, at distances of AO and AM from A. Prove that EF=AO.
(4 pont)
solution (in Hungarian), statistics
B. 4154. This problem is a classic: A town is surrounded by a circular wall. There are 12 guards serving on the wall. At twelve noon, each guard leaves his watchpost and starts walking the wall in some direction, at a speed at which it would take exactly one hour to walk around the whole town. If two guards meet, they both turn around immediately and walk at the same speed in the opposite direction. Prove that at twelve midnight each guard will be back at his watchpost.
(5 pont)
solution (in Hungarian), statistics
B. 4155. Solve the following equation:
a2b2+b2c2+c2a2+a2+b2+c2+4(a+b+c)+12=6abc+4(ab+bc+ca).
(5 pont)
solution (in Hungarian), statistics
B. 4156. Solve the following equation:
(3 pont)
solution (in Hungarian), statistics
B. 4157. Solve the following equation: [x]=x4-2x2. [x] denotes the greatest integer that is not greater than x.
Based on a competition problem from Transsylvania
(4 pont)
solution (in Hungarian), statistics
B. 4158. The midpoint of the line segment AB on the face ABCD of a cube is F. The cube is cut into two parts with a plane passing through the line segment CF, such that the ratio of the volumes of the parts containing B and D, respectively, is 1:2. Find the angle enclosed between the plane and the face ABCD.
(5 pont)
solution (in Hungarian), statistics
B. 4159. In triangle ABC, a=2b. Given the vertices A, B and a line passing through vertex C, construct the triangle.
(3 pont)
solution (in Hungarian), statistics
B. 4160. Is there a bounded set of points in the plane that has infinitely many axes of symmetry but is not centrally symmetric?
Suggested by L. Pósa
(5 pont)
solution (in Hungarian), statistics
B. 4161. Assume that a set S obtained by leaving a finite number of positive elements out of the set of natural numbers is closed under addition. Let k be an element of S. If k is subtracted from each element of S, in how many cases will the result not belong to S?
(3 pont)
 |
Problems with sign 'A'Deadline expired on March 16, 2009. |
A. 473. Show that the spherical triangles with equal area can be dissected into each other; in other words, any two spherical triangles, having the same area, can be decomposed into spherical polygons such that the two decompositions consist of the same number of pieces and the respective pieces are congruent.
(5 pont)
A. 474. The point Q is located in the convex n-gon . Show that
(The indices are considered modulo n, e.g. P0=Pn and Pn+1=P1.)
(5 pont)
A. 475. To each vertex of a regular n-gon a real number is assigned in such a way that the sum of all n numbers is positive. If three consecutive vertices are assigned the numbers x, y, z respectively and y<0 then the following operation is allowed: the numbers x, y, z are replaced by x+y, -y, z+y respectively. Such an operation is performed repeatedly as long as at least one of the n numbers is negative. Determine whether this procedure necessarily terminates after a finite number of steps.
(5 pont)
Upload your solutions above.
