KöMaL Problems in Informatics, May 2009

Problems with sign 'I' Deadline expired on June 15, 2009.

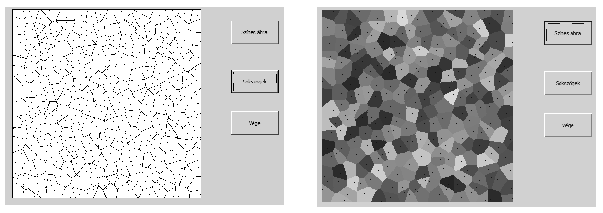
I. 214. There are N points in a square arranged arbitrarily. One can always draw a polygon around each point such that interior points of this polygon are closer to the actual point that to any other of the N-1 points. These polygons are convex and completely fill the square.

Given a square of size M×M (10M600), your program should randomly place N points (2N150) inside the square, then draw the net of polygons graphically and color them also randomly. The original N points should be clearly visible.

In the example, buttons read as ``With colors'', ``Polygons'' and ``Quit''.

The source code of your program (i214.pas, i214.cpp, ...) and a short documentation (i214.txt, i214.pdf, ...) should be submitted, also describing your solution and specifying the name of the developer environment to use for compiling.

(10 pont)

solution (in Hungarian), statistics

I. 215. Notice that the following exercise is quite similar to our earlier problem I. 202., this time however you have to use different tools.

We are given some heaps of stones. In every step, we remove one stone from each heap and form a new heap out of these stones. The order of heaps is irrelevant.

In the example, ``A kupacokban a kavicsok száma'' means ``Number of stones in the heaps'', while ``Következő lépésben'' is ``Number of stones in the next step''.

The number of steps can be arbitrary. Since the number of stones is finite, sooner or later the distribution of stones in heaps becomes cyclic.

Prepare a spreadsheet so that the number of stones in each heap can be entered into cells A1:Y1. The following 100 lines should then show the distribution of stones in the next steps. Numbers in each line should be sorted into descending order.

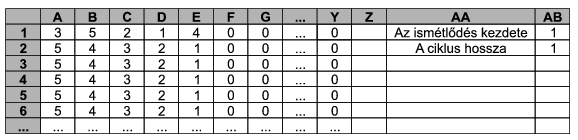
In the table, ``Az ismétlődés kezdete'' means ``Repetition begins at step'' (with the corresponding number in cell AB1), and ``A ciklus hossza'' is ``Length of the cycle'' (to appear in cell AB2).

The total number of stones is at most 25 (you do not have to check this condition). The solution should not use any macros or your own functions.

The sheet (i215.xls, i215.ods, ...) together with a short documentation (i215.txt, i215.pdf, ...) should be submitted, also containing a brief description of your solution and the name of the spreadsheet application.

(10 pont)

solution (in Hungarian), statistics

I. 216. In our March issue we have played the game MasterMind. A friend of us claims that he uses the following simple algorithm to play: he always chooses the first item from the lexicographically ordered list of possible guesses. To find out whether he indeed follows this strategy, write your program that gives the necessary number of steps in the proper order for each secret sequence.

Your program reads one line from the standard input, containing the secret sequence (without spaces). The output should be written to the standard output in n+1 lines, where n denotes the number of steps necessary to solve the puzzle.

For example, if the secret code is ``DADA'', then your output should be the following:

The source code of your program (i216.pas, i216.cpp, ...) and a short documentation (i216.txt, i216.pdf, ...) should be submitted, also specifying the name of the developer environment to use for compiling.

(10 pont)

solution (in Hungarian), statistics

Problems with sign 'S' Deadline expired on June 15, 2009.

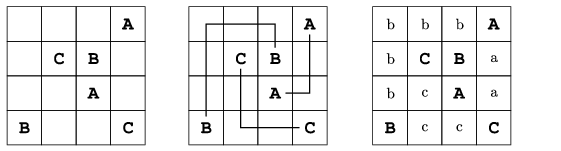
S. 45. In some quiz magazines one often sees the following ``connect the letters'' game. Given an N×N square with some letters, your task is to connect identical letters in such a way that your lines neither intersect nor overlap each other. Prepare a program that connects each pair of identical letters on a board of size at most 20×20 in the above way, if possible, otherwise, it should connect as many pairs as possible according to the rules.

The first command line argument to your program specifies the name of the text file describing the board. This input file has N lines (provided that the board is of size N×N). Each line contains N characters. Letters to be connected are denoted by uppercase letters of the English alphabet (but at most 25), while empty squares are denoted by spaces.

The second command line argument to your program gives you the name of the text file into which your solution should be written. Your solution is the board full of letters: connecting lines between the given uppercase letters are denoted by the corresponding lowercase letters. If a complete solution does not exist, a message such as ``k pair(s) of letters can not be connected'' should be printed to the standard output. The output file in this case should contain only a board that is partially filled in, but with the highest possible number of pairs connected.

The source code of your program (s45.pas, s45.cpp, ...) and a short documentation (s45.txt, s45.pdf, ...) should be submitted, also describing briefly your solution and specifying the name of the developer environment to use for compiling.

(10 pont)

statistics