KöMaL Problems in Informatics, December 2009
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'I'Deadline expired on January 11, 2010. |
I. 226. Due to economic reasons, the management of a certain company has decided to use some large capacity printers instead of many smaller printers. Larger printers can handle more complex tasks and they are faster and cheaper. A severe drawback is however that sometimes one should wait if several colleagues want to print simultaneously.
In order to minimize loss of printing time, they have installed two identical paper trays in the printer. (The printer switches between these trays automatically and instantaneously. Empty trays are immediately refilled.)
Incoming printing requests of a particular day have been recorded in the file feladat.txt in chronological order. The first number in the first line of this file is the number of seconds required for the printer to print a single page, while the second number is the capacity of a paper tray. The following lines describe the printing queue: the first 3 numbers in each line refer to the time (hour, minute, second) of the incoming printing request, then the number of pages to be printed (at most 100) and the owner are listed. We know that the company has at most 24 employees.
For example,
feladat.txt
|
The fourth row in the example feladat.txt says that Dominik wanted to print 10 pages at 8:22:26. We also see that this task required 30 seconds.
Create your program nyomtat to solve the following exercises. (Your program should process each correct input file.) Display the number of each question before solving it. If your program needs user input, print the corresponding message clearly. (In the second task, for example, ``2nd task: Please enter the name of an employee.'') You may omit diacritical marks.
1. Read the file feladat.txt and use that information to solve the following questions. (If, for some reasons, the file can not be read, enter 10 lines manually and use that data in the following.)
2. Ask the user to enter the name of an employee, then display on the screen when that employee issued a printing request. Each request should appear in different lines in hour:minute:second format.
3. Create a summary of the number of printing requests in a given hour. Each line of your output should contain the hour and the number of printing requests. Ignore those hours when there was no printing.
4. List the names of those people who already printed before 9 o'clock. Names should appear alphabetically and separated by a space.
5. List those printing tasks during which switching between paper trays was necessary. The number of those tasks should appear on the screen separated by a space.
6. Create a summary for each printing task by using the following information: time of incoming printing request, the time when the printer started and finished printing that task, further, the owner of the task. These data should be written to the file kesz.txt (each task in a separate line).
kesz.txt
|
The source code (i226.pas, i226.cpp, ...) together with a short documentation (i226.txt, i226.pdf, ...) -- also describing which developer environment to use for compiling, further a brief description of your solution -- should be submitted in a compressed file (i226.zip). feladat.txt
(10 pont)
solution (in Hungarian), statistics
I. 227. By using a spreadsheet application, compute the final results of a three-round contest. In each round, contestants should solve 3 problems. Each problem is worth at most 10 points. These points add up to stage points. The result of the contest is calculated by using stage points according to the description below.
All data and computations should be written on the sheet Verseny. Cells A1:J1 should contain some possible surnames, while cells below should contain some given names. Then in cells A6:A25 a random combination of given names and surnames should appear: they will be our contestants. The content of cells A5:K5 should be Name, Task I/1, Task I/2, ..., Task III/3, Result. Cells B6:J25 should contain random integers between 0 and 10 (inclusive): these will be the points of contestants for the tasks.
Cells K6:K25 should contain the final evaluation of the contestants. Their position at the end of each round is determined by the sum of points obtained in that round. The winner(s) of a round get(s) 1 stage point, the player in the second place gets 2 stage points, and so on, in each round. Then the sum of stage points obtained during the 3 rounds is formed. From this number, ``5'' is subtracted for each task whenever a player solved that particular task with maximal points alone; conversely, ``5'' is added to the sum of stage points for each task whenever a player obtained 0 points for that particular task (that is, failed to solve the task). Players are then sorted into ascending order according to these modified stage points: the first prize(s) go(es) to the player(s) with the less (modified) stage points, the second prize to those with the second less points, and the third prize to those with the third less points. This text should appear in the appropriate line of column K. Further, players in the following three places obtain a Distinction. They too should be listed in column K.
You should not use macros or program modules, only formulae and built-in functions. For auxiliary computations, use only the part of the sheet Verseny below line 30.
Your spreadsheet (i227.xls, i227.ods, ...) together with a short documentation (i227.txt, i227.pdf, ...) -- also describing the name and version number of the spreadsheet application, further a brief description of your solution -- should be submitted in a compressed file (i227.zip).
(10 pont)
solution (in Hungarian), statistics
I. 228. Two players play the following game. There is an even number of stones in a row, each with a known mass. Players in turn take one stone from either end of the row. If there are no more stones left, both players sum the masses of their stones. The winner is who possesses the bigger sum.
Prepare a version of this game which can be played on a web page. Draw the stones together with their masses. If the user clicks on a stone at the end of the row, then that stone should disappear and its mass should be added to the player's sum. If there are no more stones left, your program should display the winner. One of the players should be the computer itself, beginning the game.
Your program should use 16 stones. The computer's strategy (being the winning strategy) should be the following: the starting player sums the masses of stones at even and at odd positions, then takes a stone at the end of the row from the group for which this sum is greater. (In case of equality, the choice is arbitrary.)
You can use HTML and JavaScript elements in your solution.
The file i228.html together with any auxiliary GIF, JPEG or PNG images should be submitted together with a short documentation (i228.txt or i228.pdf) in a compressed folder i228.zip.
(This exercise is based on a problem of the International Olympiad in Informatics 1996.)
(10 pont)
 |
Problems with sign 'S'Deadline expired on January 11, 2010. |
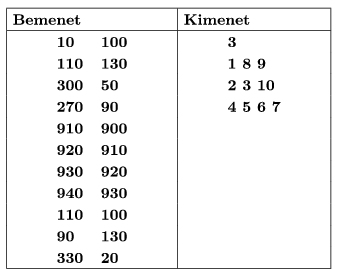
S. 49. People in a remote country care for the environment and are planning to use vehicles powered by hydrogen. Liquid hydrogen is stored in safety tanks, unfortunately however, there are still only few hydrogen stations. Hydrogen cars can operate in regions where hydrogen stations are at most K km apart from each other. Note however that they use the following metric in the coordinate plane: the distance of two points is the sum of absolute value of differences of the corresponding coordinates, |x1-x2|+|y1-y2|.
Your task is to group hydrogen stations: two stations will be in one group if one can travel between the two stations by touching stations in the group being at most K km apart. Your program should compute the number of these groups, further, give which stations are part of one group.
The first command line argument to your program is the name of the input file. The first line of this file gives the number of hydrogen stations N (3 N
N 200), further the value of K (100
200), further the value of K (100 K
K 500). The following N lines then contain the x, y (0
500). The following N lines then contain the x, y (0 x,y
x,y 1000) coordinates of the stations.
1000) coordinates of the stations.
The second command line argument to your program is the name of the output file. The first line of the output file should contain the number of groups, G, and the next G lines should list the codes of hydrogen stations in one group, separated by a space.
In the example, ``Bemenet'' is input, while ``Kimenet'' is output.
The source code and project files of your solution -- without the .exe or any other auxiliary files generated by the compiler -- should be submitted together with a short documentation in a compressed folder s49.zip.
(10 pont)
$Var(Body)
Upload your solutions above
