KöMaL Problems in Mathematics, January 2010
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on February 10, 2010. |
K. 235. The official currency on the planet Kloppar is the tirof, for which the small change is the dimar, and there is an even smaller change called the nepi. One dimar is worth a whole number of nepis, and a tirof is worth a whole number of dimars. Sangi had dinner in a restaurant on the planet. After dinner he received the following bill: Fried vondar: 7 dimars and 2 nepis; Pickled rotins: 10 dimars and 5 nepis; Vundeg bread: 1 dimar and 6 nepis; Carbonated nestaki drink: 6 dimars and 4 nepis; Krabban cake: 4 dimars; Total: 2 tirofs, 8 dimars and 1 nepi. How many dimars are worth a tirof, and how many nepis are worth a dimar?
(6 pont)
solution (in Hungarian), statistics
K. 236. The intersection of two interior angle bisectors of a parallelogram lies on a side of the parallelogram. In what ratio does the point of intersection divide the side?
(6 pont)
solution (in Hungarian), statistics
K. 237. Customers at a parking lot are charged 120 forints (HUF, Hungarian currency) an hour for parking between 8 a.m. and 6 p.m. They need to insert at least 30 forints in the parking meter, and the longest possible period covered by a ticket is 3 hours. The meter takes 10, 20, 50 and 100-forint coins. During the coins being inserted, the meter continually displays the end of the parking time covered by the money inserted. The end of the parking time must not extend further than 6:00 p.m. (that is, at 17:15 p.m. the meter does not accept a 100-forint coin any more.)
a) In what time interval is it impossible to obtain a valid parking ticket from the meter?
b) A customer is standing in front of the meter at 11:28 a.m. He would like to stay till 7 p.m. How many times should he throw money in the meter, when, and how much if he wants to minimise the number of visits to the meter but does not want to park (not even for a single minute) without a valid ticket?
(6 pont)
solution (in Hungarian), statistics
K. 238. The centre of the regular pentagon ABCDE is the point O. Each of the points A, B, C, D, E, O is coloured red, yellow, blue or green (each point is given a single colour), so that none of the triangles OAB, OBC, OCD, ODE, OEA has two vertices of the same colour. In how many different ways is that possible?
(6 pont)
solution (in Hungarian), statistics
K. 239. Someone bought a bar of chocolate, and then realised that the same chocolate in another shop cost as many percent more, as the price in forints (HUF, Hungarian currency) that he had paid for it. How much did he pay for the chocolate if it cost 75 forints in the other shop?
(6 pont)
solution (in Hungarian), statistics
K. 240. A company of T members went on a trip to the countryside. Exactly half of them went on foot. The distance to the destination was T kilometres along the footpath, and they covered it in 1 hour. The other half of the company went by bike along another route. Their speed (not counting periods when they stopped) was T less than T times the speed of the walkers.
The bikers had to stop on their way for T minutes because of a flat tire, and later on they had to stop again, for T times as much time, because of a broken chain on another bike. When they continued the journey, a biker with no technical problems so far took the lead of the group for T minutesminutes, and then let somebody else to take the lead. Finally, the bikers arrived at the destination T minutes sooner than the walkers. How long was the footpath, and how long was the bike route?
(6 pont)
 |
Problems with sign 'C'Deadline expired on February 10, 2010. |
C. 1015. If the sum of its digits is added to a certain three-digit number, the resulting number consists of identical digits. If the sum of the digits is subtracted from the original number, the result will also consist of identical digits. What is the original number?
(5 pont)
solution (in Hungarian), statistics
C. 1016. In a right-angled triangle ABC, there is a 30o angle at vertex B. D is the centre of the square drawn on the outside to the hypotenuse BC. Find angle 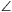 ADB.
ADB.
(5 pont)
solution (in Hungarian), statistics
C. 1017. The two cubes shown in the diagram are lying on a horizontal tabletop. The sum of their edges is 2 cm, and the sum of their volumes is 5.375 cm3. Find the area of the black rectangle.
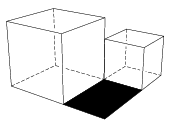
(5 pont)
solution (in Hungarian), statistics
C. 1018. A group of 5 little girls and 7 little boys in the kindergarten are playing at weddings. They choose a bride and groom, a registrar, two bridesmaids, one best man for the bride and one for the groom, one witness for the bride and one for the groom. Three of the girls each have a brother in the group, too, and there are no other pairs of brothers or sisters. In how many different ways can the selection be made if a sister and brother cannot play the bride and groom, and the registrar cannot be the brother or sister of either of the newly weds. (Bridesmaids are girls and best men are boys. There is no restriction on the sex of the witnesses.)
(5 pont)
solution (in Hungarian), statistics
C. 1019. A cylinder lying on a horizontal plane is held fixed by placing a prism against each side. (The prisms touch the lateral surface of the cylinder along an upper edge.) What is the radius of the cylinder if the heights of the prisms are 9 cm and 2 cm, and their separation is 23 cm?
(5 pont)
 |
Problems with sign 'B'Deadline expired on February 10, 2010. |
B. 4232. Two sailboats are travelling in perpendicular directions on the lake Balaton at the same speed of 10 km/h. At a given time instant, while both are approaching the intersection of their paths, the respective distances of sailboats \(\displaystyle A\) and \(\displaystyle B\) are 1 km and 2 km from that point. A man travelling in boat \(\displaystyle A\) wants to swim to boat \(\displaystyle B\). He swims at a uniform speed of 2 km/h. When should he jump in the water in order to minimise the time spent in the water?
Suggested by L. Koncz
(4 pont)
solution (in Hungarian), statistics
B. 4233. The three-element subsets of a seven-element set are coloured. If the intersection of two sets is empty then they have different colours. What is the minimum number of colours needed?
(4 pont)
solution (in Hungarian), statistics
B. 4234. All possible strings of \(\displaystyle n\) different letters are formed out of a \(\displaystyle k\)-element alphabet. Two such strings are connected with an edge if they only differ in a single position. What is the diameter of the resulting graph?
CIIM, Columbia, 2009
(4 pont)
solution (in Hungarian), statistics
B. 4235. The sides of a convex quadrilateral \(\displaystyle ABCD\) are divided into \(\displaystyle n\ge 2\) equal parts. On the sides \(\displaystyle AB\), \(\displaystyle BC\), \(\displaystyle CD\), \(\displaystyle DA\), let \(\displaystyle A_k\), \(\displaystyle B_k\), \(\displaystyle C_k\), \(\displaystyle D_k\) denote the \(\displaystyle k\)th points of division, counting from the vertices \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\), \(\displaystyle D\), respectively. For which pairs \(\displaystyle (n,k)\) is it true that the quadrilateral \(\displaystyle ABCD\) is a parallelogram if and only if the quadrilateral \(\displaystyle A_kB_kC_kD_k\) is also a parallelogram?
Suggested by G. Mészáros, Kemence
(3 pont)
solution (in Hungarian), statistics
B. 4236. Let \(\displaystyle a\), \(\displaystyle b\) and \(\displaystyle c\) be the sides of triangle \(\displaystyle ABC\), let \(\displaystyle f_a\), \(\displaystyle f_b\) and \(\displaystyle f_c\) denote the lengths of the interior angle bisectors, and let \(\displaystyle t_a\), \(\displaystyle t_b\) and \(\displaystyle t_c\) be the segments of the interior angle bisectors that lie inside the circumscribed circle. Show that \(\displaystyle a^2b^2c^2= f_af_bf_ct_at_bt_c\).
(Mathematics Magazine, 1977)
(3 pont)
solution (in Hungarian), statistics
B. 4237. Let n be a positive integer. Determine the sum of all fractions , such that the numbers x and y are relative primes, are not greater than n, and their sum is greater than n.
(5 pont)
solution (in Hungarian), statistics
B. 4238. Show that the points of the curve of equation lie on a parabola.
(4 pont)
solution (in Hungarian), statistics
B. 4239. Solve the equation 8x(2x2-1)(8x4-8x2+1)=1.
(5 pont)
solution (in Hungarian), statistics
B. 4240. The planes S1 and S2 intersect in a line m. Line e intersects plane Si at the point Di. The angle enclosed by e and Si is 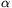 i. Show that if D1
i. Show that if D1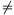 D2, then
D2, then 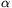 1>
1>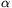 2 holds true if and only if D1 lies closer to m than D2.
2 holds true if and only if D1 lies closer to m than D2.
(4 pont)
solution (in Hungarian), statistics
B. 4241. Let p1=2, and for n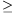 1 let pn+1 denote the smallest prime factor of the number
1 let pn+1 denote the smallest prime factor of the number . Prove that every prime number occurs in the sequence
(5 pont)
 |
Problems with sign 'A'Deadline expired on February 10, 2010. |
A. 497. There is given an acute triangle ABC in the plane. Denote by A1, B1 and C1 the perpendicular feet of an arbitrary interior point P of the triangle on the sides BC, CA and AB, respectively. Let the inradii of the triangles PAC1, PC1B, PBA1, PA1C, PCB1 and PB1A be 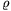 1,
1,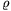 2,...,
2,...,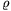 6, respectively. Determine the locus of those points P for which
6, respectively. Determine the locus of those points P for which
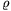 1+
1+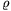 3+
3+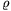 5=
5=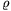 2+
2+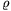 4+
4+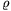 6.
6.
Proposed by Viktor Vígh, Szeged
(5 pont)
solution (in Hungarian), statistics
A. 498. Let p(x) be a polynomial with integer coefficients, and let w be a complex number of unit absolute value. Prove that if the number c=p(w) is purely real, then there is a polynomial q(x) with integer coefficients for which .
(5 pont)
A. 499. Prove that there exist positive constants c and n0 with the following property. If A is a finite set of integers, |A|=n>n0, then
|A-A|-|A+A| n2-cn8/5.
n2-cn8/5.
Miklós Schweitzer Memorial Competition, 2009
(5 pont)
Upload your solutions above.
