KöMaL Problems in Physics, September 2010
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'M'Deadline expired on October 11, 2010. |
M. 307. Measure the refractive indices of different liquids (e.g. water, glycerin) in the following way: place a concave mirror (a watch glass can also be used) to the table create the sharp image of a filament lamp, hanging from the ceiling, on a screen made of tracing paper (translucent paper). Then pour some liquid into the mirror and find the sharp image of the filament lamp again. Measuring distances determine the refractive index of the liquid.
(6 pont)
 |
Problems with sign 'P'Deadline expired on October 11, 2010. |
P. 4264. By what percent would the value of the acceleration due to gravity change on the North-pole if the radius of the Earth was increased by 1%, while its mass remained the same.
(3 pont)
solution (in Hungarian), statistics
P. 4265. A 200 m-long car convoy is travelling at a speed of 10 m/s. From the end of the convoy a motorbike starts to move to the front of the convoy at a speed of 20 m/s.
a) How long does it take to reach the front of the convoy?
b) How long does it take to go back?
(3 pont)
solution (in Hungarian), statistics
P. 4266. The pulling force that an electric engine can exert when its speed is 57.6 km/h is 310 kN. The voltage is 3.6 kV, and the current in all the eight electric motors is 230 A. Determine the efficiency of the engine.
(3 pont)
solution (in Hungarian), statistics
P. 4267. The original length of a spring is 25 cm. It elongates 2 cm if a force of 1 N is exerted on it. A container is filled with water and one end of the spring is fixed 30 cm above the surface of the water in the container. A wooden block of mass 32 g and of density 0.4 g/cm3 is hanged onto the other end of the spring. The height of the block is 5 cm. To what depth does the block emerges into the water?
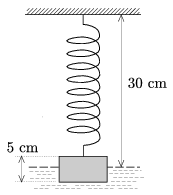
(4 pont)
solution (in Hungarian), statistics
P. 4268. A physics teacher often went to skate to a nearby frozen lake. Once he could reduce his speed to one third of its original value along 16 m skidding, and then it took him 1 more second to stop. How much distance did he cover during the braking. On another day he had the same initial speed and suddenly he noticed a crevasse in the ice 20 m in front of him. At what distance from the crevasse could he stop, if his reaction time is 0.1 s, and he used his familiar braking technique.
(4 pont)
solution (in Hungarian), statistics
P. 4269. 4 kJ heat is added to a sample of gas whose original temperature is 300 K. Both the volume and the pressure of the gas is doubled, and the gas does 1 kJ work on its environment during the process. The graph of the process on the p-V diagram is a straight line.
a) How many moles of gas are there in the sample?
b) How many atoms constitute one molecule of the gas?
(4 pont)
solution (in Hungarian), statistics
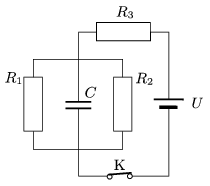
P. 4270. The switch in the circuit, shown in the figure has been closed for quite a long time. (U=100 V, C=2 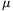 F, R1=20
F, R1=20 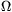 , R2=30
, R2=30 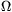 , R3=12
, R3=12 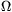 .)
.)
a) Determine the charge on the capacitor.
b) The switch is opened. What amount of charge flows through the resistor R1 after opening the switch?
c) How much work is done on the resistor R1 after opening the switch?
(4 pont)
solution (in Hungarian), statistics
P. 4271. There is a pair of parallel, horizontal, conducting rails in uniform vertically downward magnetic field of induction B=0.5 T. The two rails are at a distance of  =10 cm and they are connected to a rechargeable battery of potential difference U0=12 V. A metal rod of mass m=50 g, and of resistance R=2
=10 cm and they are connected to a rechargeable battery of potential difference U0=12 V. A metal rod of mass m=50 g, and of resistance R=2 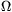 , is placed onto the rails, perpendicularly to them. The coefficient of friction between the rod and the rails is
, is placed onto the rails, perpendicularly to them. The coefficient of friction between the rod and the rails is 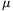 =0.3.
=0.3.
a) What is the initial acceleration of the rod when switch K is closed?
b) What would the final speed of the rod be if the rails are very long?
c) Estimate, (try to give a precise estimation) the covered distance, and the time during which the speed of the rod increases from to
.
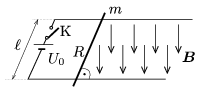
(5 pont)
solution (in Hungarian), statistics
P. 4272. We have 4 alike, ideal diodes in order to rectify the sinusoidal voltage of the mains. The r.m.s. value of the mains is 230 V, and its frequency is 50 Hz. (Any number of diodes can be used up to 4.)
a) What circuit would you build in order to make a half-wave rectifier?
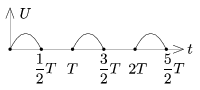
b) What circuit would you build in order to make a full-wave rectifier?
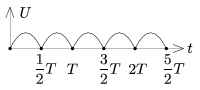
c) Determine the r.m.s. value of the voltage in both cases.
(4 pont)
solution (in Hungarian), statistics
P. 4273. Two unknown impedances are connected in parallel to the mains, of voltage 230 V and of frequency 50 Hz. The maximum value of the current in the main branch is 20 A. The current through one of the impedances leads the current in the main branch by an angle of , and through the other impedance the current lags behind the current in the main branch by an angle of
.
a) What are the instantaneous current values in the two branches at t=0.01 s, if the current in the main branch is zero at t=0?
b) What are the values of the inductance and the capacitance in the two branches?
(5 pont)
Upload your solutions above.
