Problems in Physics, October 2010

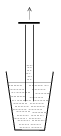
M. 308. Close the top end of a glass tube, open at its both ends, and push it vertically into a bucket of water. Suddenly open the top end of the tube. Examine how the height of the first highest water level depends on the length of that part of the tube which is immersed into the water. Use several tubes of different diameters.

(6 points)

P. 4274. It is known that we can look through the glass of an ordinary window. What happens when the glass cracks? The crack can be noticed immediately. What is the reason?

(3 points)

P. 4275. The pressure of a sample of ideal gas in a container of 10 litres is 1.6 MPa, and its temperature is 25 ^oC. How many numbers of moles of gas are there in the container? What is the density of the gas if 10% of the mass of the gas is Helium and the rest is Nitrogen?

(4 points)

P. 4276. At what angle can a ladder of weight G be leaned against the vertical smooth wall, if a man of mass m can safely climb up on it? The coefficient of static friction between the ground and the ladder is 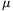₀.

(4 points)

P. 4277. The wedge shown in the figure can slide without friction on a horizontal tabletop. The mass of the wedge is M and its angle of elevation is =30^o. A body of mass m slides down without friction along the wedge, the path of the body makes an angle of 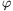=60^o with the ground. Find the ratio of the masses, m/M.

(5 points)

P. 4278. A U-shaped communicating vessel, made of a bent glass tube, contains water. The part of the tube which is filled with water is 30 cm long. The difference between the levels of the water in the two parts of the tube is 1 cm when the communicating vessel is in a vehicle which accelerates uniformly.

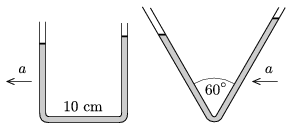
What is the acceleration of the vehicle if the length of the part of the tube which is horizontal is 10 cm? What would have the difference between the lengths of the water columns been, if a V-shaped communicating vessel had been used in which the total length of the tube which is filled with water was also 30 cm?

(5 points)

P. 4279. A rubber ball is dropped in a lift, which is at rest, from a height of 2 meters, and first it bounces back to a height of 162 cm. How much time elapses between the first and the second bounces? Then the experiment is repeated, such that the lift accelerates upward with a constant acceleration of 1 m/s². Will the rebouncing heights and the time between two consecutive bounces change? If yes, how?

(5 points)

P. 4280. On object is projected horizontally from a tower and it hits the ground 40 m from the foot of the tower at an angle of 45^o. (Air-drag is negligible.) a) From what height is the object projected? b) From what height should the object be projected with the same initial horizontal speed, in order that the ratio of the horizontal and vertical displacements of the object should be the reciprocal of those of the former ones?

(4 points)

P. 4281. Using six different resistors the tetrahedron ABCD was soldered. If a battery is inserted between two vertices (for example A, B) and a sensitive ammeter is inserted between other two vertices (C, D), then we experience with a surprise that the ammeter reads zero, independently of the two vertices of the tetrahedron which were chosen first.

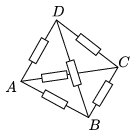
What is the relation between the six resistances?

(4 points)

P. 4282. Suppose that Aluminum balls of different sizes get into the space from the International Space Station. The smaller or greater mass balls cool more quickly?

(4 points)

P. 4283. The bindings of Deuterium and Tritium nuclei are not so strong as that of the nucleus of the Helium, that is why quick neutrons are ejected when Tritium is bombarded with an electrically accelerated beam of Deuterium. The reaction is the following: ²H+³H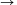⁴He+n. (The kinetic energy of the deuteron is negligible with respect to its binding energy.) Determine the kinetic energy of the quick neutrons.

(4 points)