KöMaL Problems in Informatics, November 2010
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'I'Deadline expired on December 10, 2010. |
I. 250. We would like to model the spread of cracks on a rectangular plate of size \(\displaystyle N\times M\) (\(\displaystyle 5\le N,M\le 100\)).
First fill the rectangle with random integers between 0 and 99. Cracks will emerge from boundary points having the largest numbers. (If there are more maximal numbers on the boundary, more cracks will be initiated simultaneously.) The direction of the spread of a crack depends on the orientation of the side they were born on: a crack coming from below can spread only upwards, to the left or to the right. If a crack started from the right, it can only move to the left, upwards or downwards. (Cracks coming from the other directions follow a similar rule.)
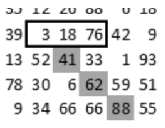
In the first example, the crack started from below. The 3 possible next steps are framed.
The crack will move into the direction determined by the largest of the 3 possible numbers. If there are identical numbers among them, the crack will bifurcate into the corresponding directions. A crack stops, if it reaches the boundary of the rectangle or runs into another already existing crack.
Your program should simulate and show the spread of the cracks on the \(\displaystyle N\times M\) rectangle.
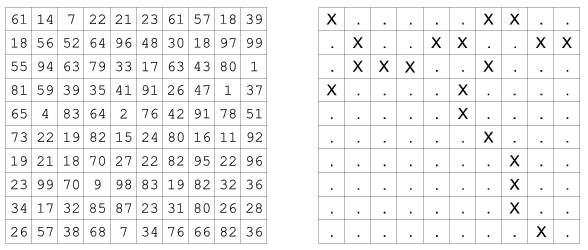
The first two arguments to your program should be \(\displaystyle N\) and \(\displaystyle M\), while the third one should be the name of an output file. The output file should contain the matrix of your random numbers and the cracks similarly to the second example. (Cracks are denoted by ``X'' characters, the other squares contain ``.'' characters. Numbers and these characters should be separated by a space.) This example shows a possible final state on a \(\displaystyle 10\times 10\) rectangle.
The source code (i250.pas, i250.cpp, ...) together with a short documentation (i250.txt, i250.pdf, ...) -- also describing which developer environment to use for compiling, further a brief description of your solution -- should be submitted in a compressed file (i250.zip).
(10 pont)
solution (in Hungarian), statistics
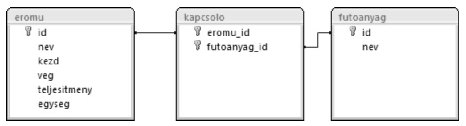
I. 251. The files eromu.txt, kapcsolo.txt and futoanyag.txt (tabulator separated text files in UTF-8 encoding with field names in their first lines) contain data about Hungarian power plants.
[1.] Prepare a database with name i251. You should import the above 3 files into this database without changing their names.
[2.] Upon importing, you should set the appropriate data formats and keys. No new fields should be created in the tables.
Tables

Now solve the following task. When a query is answered, no other data, only the requested results should appear. Queries should be named as indicated in the parentheses.
table
[3.] By using a query, list in alphabetical order the names of renewable energy plants (that is, fueled by biomass or water). (3megujulo)
[4.] Which power plant has the largest power? List its name and power. (4legnagyobb)
[5.] Determine by a query which power plants are fueled by the same method as ``Mátrai Erőmű''. (5matrai)
[6.] For each fuel type, determine the total power of the power plants supposing that only that fuel type is available. This list of fuel types and total power should be sorted into decreasing order according to ``power''. (6tipusonkent)
[7.] Make a query to list the number of power plants put in operation in each decade. (7szakaszok) For example, the ``60s'' denote years between 1960 and 1969.

[8.] The side-effect of fuelling a power plant with brown coal is the production of a large amount of carbon dioxide, moreover, they have little efficiency, so these power plants will be abolished. To maintain the database, you should create 3 deletion queries assuming consecutive execution. You do not have to execute the deletion queries, but it not forbidden.
[\(\displaystyle a.\)] By using a query, delete records from table kapcsolo which had any connection to using brown coal. (8barna_1)
[\(\displaystyle b.\)] Delete the record of brown coal from table futoanyag (8barna_2)
[\(\displaystyle c.\)] Delete from table eromu all data in connection with power plants to be abolished due to the fact of having no other fuel sources. (8barna_3)
The database (i251.odb, i251.mdb) together with a short documentation (i251.txt, i251.pdf) -- also containing the name and version number of the database application -- should be submitted in a compressed file (i251.zip).
(10 pont)
solution (in Hungarian), statistics
I. 252. The link http://jeanettteigen.files.wordpress.com/2010/10/eating-above-manhattan-post2.jpg contains a famous image about relaxing workers in Manhattan. You should modify this image such that your fellows appear on the image instead of those workers. None of the original workers should be visible, only a friend of yours or the background. You can also add a new part of a building or background to the image such that, for example, an unnecessary leg is removed. Your final 800×600 grayscale image should be similar to the original one. You should use the freely downloadable image manipulation program Gimp (http://www.gimp.org).
The resulting Gimp file (i252.xcf) together with your original image containing your friends (i252tars.jpg), both in 800×600 pixels, should be submitted in a compressed file i252.zip with size under 2 MB.
(10 pont)
 |
Problems with sign 'S'Deadline expired on December 10, 2010. |
S. 57. We would like to cover a chessboard with dominoes (without gaps or any overlapping) in such a way that some squares of the board are previously excluded (so that no domino can be put on those squares).
Your program should read the size of the board and the excluded squares from the standard input, then compute a suitable cover, if it exists.
The structure of the input is the following: the first line contains two integers separated with a space, denoting the size of the board (\(\displaystyle 1\le N \le 100\)) and the number of excluded squares (\(\displaystyle 0 \le M \le N\cdot N\)). Then each of the following \(\displaystyle M\) lines contains the row and column coordinates of the excluded squares (again, separated with a space).
If there exists a suitable cover, then your program should write \(\displaystyle N\) lines to the standard output, with each line having \(\displaystyle N\) numbers. The number in the \(\displaystyle i^{\rm th}\) row and \(\displaystyle j^{\rm th}\) column gives the number of the domino covering the \(\displaystyle i^{\rm th}\) row and \(\displaystyle j^{\rm th}\) column of the chessboard, if that square is not excluded, otherwise that number should be 0. Numbering of the dominoes is arbitrary (different dominoes however should have different numbers). If there is no solution, you should display the message ``this board can not be covered''. The time limit for your program in each test case will be at most 10 seconds.
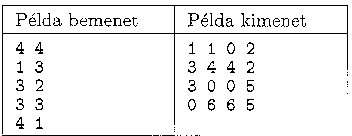
In the example, ``Példa bemenet'' is the sample input, while ``Példa kimenet'' is the corresponding output.
The source code and project files of your solution -- without the .exe or any other auxiliary files generated by the compiler -- should be submitted together with a short documentation in a compressed folder s57.zip. One can obtain 8 points if the program can solve any test cases of the above type within 10 seconds. (If the running time exceeds 10 seconds, we will consider that test case unsolved.) 5 points can be awarded if your program can cover boards of size at most 10 by 10. Further 2 points can be obtained for documentation.
(10 pont)
$Var(Body)
Upload your solutions above
