KöMaL Problems in Informatics, December 2010
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'I'Deadline expired on January 10, 2011. |
I. 253. In this exercise the last street of a little village is considered. Houses are located only on one side of the street, with each having a painted wooden fence. Each fence has a single color and houses are not directly adjacent to the front fences.
The file utca.txt describes properties of the fences for each house in order: each line of the file contains 2 integers and a word of at most 20 characters. The first number is the length of the front fence in meters (the other dimension of the rectangular house lots is the same in each case), the second number is the distance of the front gate from the corner of the lot. The gate is now considered to be a single point in this model and never touches the common boundary of two lots. The word describes the color of the fence. The length of the street is at most 10 km.
According to the second line of the example, the second house lot in the street has front length of 18 m, and its gate is located 5 m from the corner (therefore the distance between the gate and the end of the street is 20 m).
15 3 sarga
18 5 kek
11 4 sarga
...
Create a program to answer the following questions. The source code of the program should be saved as porta. When writing on the screen, the number of the actual task together with the expected type of the query (e.g. ``Task #4: please enter the distance between the lamp posts'') should be displayed.
1. Read the file utca.txt and then solve the following tasks.
2. Give the number of house lots with red fence.
3. Give the ratio between the largest and smallest area of house lots, to two decimal places.
Street lighting is now being constructed in the village. A lamp post is put on the corner of this street, then the distance between successive lamp posts is given as \(\displaystyle v\) m. Each lamp is capable of illuminating a fixed length of the fences, \(\displaystyle l\) m before and \(\displaystyle l\) m after the lamp post. We know that \(\displaystyle v\) and \(\displaystyle l\) are integers with \(\displaystyle v\ge 2l\), that is, illuminated areas can not be disjoint.
4. Prompt for the values of \(\displaystyle v\) and \(\displaystyle l\). Use these values in tasks below.
5. Create a map of the street with lamp posts included in the file kep.txt. The first line should contain the fences, the second one the lamp posts. Boundaries are denoted by the ``|'' character, while fences by a space. Each fence is denoted by the starting letter of its color. Lamp posts are marked with ``O''. The example in this task corresponds to the previous example if the distance between lamp posts is 6 m. Your output should only contain the two lines with grey background.
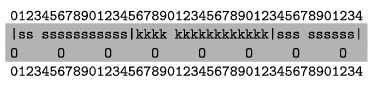
6. In order to minimize costs, if there is nobody on the street, only the minimal number of lamps should be active so that each gate is illuminated. Active lamps should be determined by the following algorithm.
Loop until there is an unilluminated gate
Locate the first such gate
Determine the last lamp which illuminates it
End of loop
The number of active lamps should be displayed and separated by a space.
7. In order to minimize costs even further, a lamp should only be active if there is somebody staying in its light cone. Determine and display the total illumination time (in minutes) if someone walks through the entire street with 100 m/s just along the fences.
The source code (i253.pas, i253.cpp, ...) together with a short documentation (i253.txt, i253.pdf, ...) -- also describing which developer environment to use for compiling, further a brief description of your solution--should be submitted in a compressed file (i253.zip).
(10 pont)
solution (in Hungarian), statistics
I. 254. The XML file format -- although sometimes hidden -- is becoming more and more widespread among different documents, like text documents, sheets or databases. Databases usually contain data in a well-defined structure. This structure is also present when using XML and is called XML schema. This special XML document has extension XSD.
You should prepare an XML schema describing some personal data of a student and their parents. (Data about studies and absences are not stored now.) Your schema should be able to handle real-life situations, a student for example can have more email addresses or phone numbers, or one of the parents may be unknown.
Mandatory data to be recorded are found in the appropriate paragraphs of the Education Law. Besides this, you should also include the number of the class and the name of the homeroom teacher of the student, further some additional data illustrating the capabilities of the schema.
You can use http://www.xmlme.com/Validator.aspx to validate your work online.
The XML schema i254.xsd and a file i254.xml containing some sample data should be submitted in a compressed file i254.zip.
(10 pont)
solution (in Hungarian), statistics
I. 255. Newton's cradle is a popular device demonstrating the principle of conservation of energy and momentum.

You should prepare a simulation with a GIF animator, like (the freely downloadable) Stykz or Pivot Stickfigure Animator programs. (Video hosting websites contain tutorials for these software.)
You should prepare 3 animations, showing the motion if 1, 2 and 3 spheres are pulled away and let to fall. Energy and momentum are considered to be perfectly conserved. An appropriate refresh rate and an infinite loop should be set for your animation.
The animations (in GIF) and the source code (in the default file format of the animator software) should be submitted together with a short documentation (i255.txt, i255.pdf, ...) -- containing the name of the software and a brief description of your solution -- in a compressed file (i255.zip).
(10 pont)
 |
Problems with sign 'S'Deadline expired on January 10, 2011. |
S. 58. The most spectacular event during the Annual Congress of Magicians is the contest of ``tall talks''. The winner is who can cast the longest magic spell consisting of a single word within a specified time limit, resulting in wonderful side effects.
Unfortunately, the contest proved to be a little too spectacular last year, and recovering the town took several months thereafter. To prevent such situations in the future, from now on magicians can only cast spells which can be written as a concatenation of some palindromes of even length, since these words are known to be harmless.
Your program should be able to prove whether a particular magic word is harmless by decomposing it, if possible, so it can be cast during the contest.
The first line of the standard input contains a single integer, the number N of magic words to be checked (1 N
N 100), which are listed in the following N lines. Words contain only lowercase letters of the English alphabet. Each word is at most 1 000 000 characters long. Harmless words are built out of palindromes of length at most 5000.
100), which are listed in the following N lines. Words contain only lowercase letters of the English alphabet. Each word is at most 1 000 000 characters long. Harmless words are built out of palindromes of length at most 5000.
The standard output should contain exactly N lines. The ith row should contain the evaluation of the ith magic word. If the word is harmless, first the number of palindromes K in its decomposition should be given (K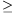 1), then elements of the decomposition should follow, separated by a space. If the decomposition is not unique, any of them can be displayed. If the word is maleficent, a ``0'' should appear.
1), then elements of the decomposition should follow, separated by a space. If the decomposition is not unique, any of them can be displayed. If the word is maleficent, a ``0'' should appear.
In the example, ``Példa bemenet'' is sample input and ``Példa kimenet'' is the corresponding sample output.

The source code and project files of your solution -- without the .exe or any other auxiliary files generated by the compiler -- should be submitted together with a short documentation (s58.txt, s58.pdf, ...) in a compressed folder s58.zip.
(10 pont)
$Var(Body)
Upload your solutions above
