A KöMaL 2011. februári informatika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
I-jelű feladatokA beküldési határidő 2011. március 10-én LEJÁRT. |
I. 259. A rekurzió a matematikában és az informatikában gyakran használt eszköz. A probléma megoldás különböző fázisaiban, így a specifikációban, az algoritmikus tervezésben és a programnyelven történő kódolásban fordulhat elő.
A specifikáció megadására függvényt szokás használni, amely a bemenet és a kimenet között hatékonyan adja meg a kapcsolatot. Kezdésként nézzük a hatványozás műveletét. Ennek definíciója: \(\displaystyle x^{n} =x\cdot x^{n-1}\), és \(\displaystyle x^{0}=1\), másképpen:
\(\displaystyle \mathop{\text{hatvány}}\, (x,n)= \begin{cases} 1 & \text{ha } n=0, \\ x\cdot \mathop{\text{hatvány}}\, (x,n-1) & \text{ha } n>0. \end{cases} \)
Így tehát az \(\displaystyle 5^{3}\)-t visszavezetjük \(\displaystyle 5\cdot 5^{2}\)-ra, vagyis \(\displaystyle 5^{2}\)-ra, azt \(\displaystyle 5^{1}\)-re, végül azt az \(\displaystyle 5^{0}\)-ra, amit már nem vezetünk vissza. A feladat rekurzív algoritmussal hatékonyan megoldható:
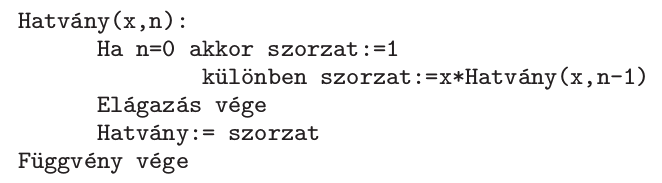
Funkcionális programozási nyelven, például Imagine Logo-ban a kódolás természetesen következik:
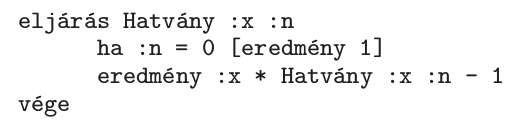
A nemrekurzív nyelvek is engedélyezhetik a kódolást, így például Pascal nyelven a kód:

Az iteratív módon meghatározott algoritmusok, programok átírhatók rekurzívvá. A legfontosabb algoritmikus egységekkel, a szekvenciával és az elágazással nincs gond, változtatás nélkül átvihetők. A ciklust tartalmazó eljárásokat kell rekurzívvá tenni. Az elöltesztelő ciklus átírása:

Minta: Állítsuk elő a természetes számok sorozatát \(\displaystyle A\)-tól \(\displaystyle B\)-ig (\(\displaystyle 1\le A,B\le 100\)). Például az Előállít(5, 10, Sor, 1) eljárás a Sor tömbbe elhelyezi az 5 6 7 8 9 10 számsort.
I. Iteratív megoldás:
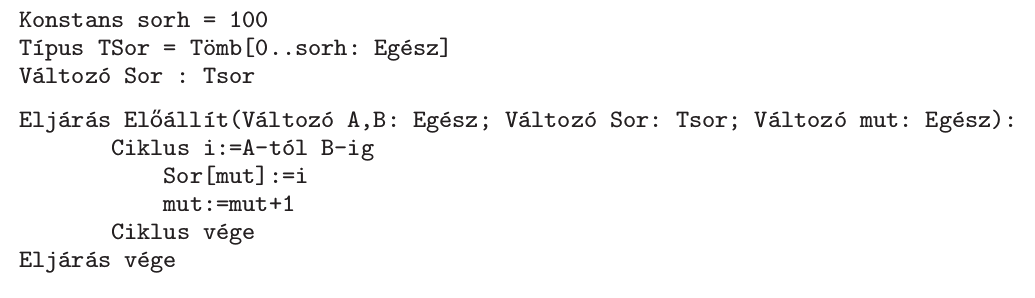
II. Rekurzív megoldás:

Készítsünk programot, amely számsorozatokat állít elő úgy, hogy a programban ciklus utasítást nem használunk.
\(\displaystyle a)\) Írjunk függvényt, ami egy \(\displaystyle N\) (\(\displaystyle N\ge 1\)) magas számhegyet hoz létre! Példa: számhegy 5 Eredménye: 1 2 3 4 5 4 3 2 1;
\(\displaystyle b)\) Írjunk függvényt, ami egy \(\displaystyle N\) magas számhegységet hoz létre! Példa: számhegység 4 Eredménye: 1 1 2 1 1 2 3 2 1 1 2 3 4 3 2 1;
\(\displaystyle c)\) Írjunk függvényt, ami egy \(\displaystyle N\) magas számlépcsőt hoz létre! Példa: számlépcső 6 Eredménye: 1 2 2 3 3 3 4 4 4 4 5 5 5 5 5 6 6 6 6 6 6;
\(\displaystyle d)\) Írjuk fel az alábbi, rekurzív képlettel megadott sorozat első \(\displaystyle N\) elemét: \(\displaystyle a_{1}=-1\) és \(\displaystyle a_{n}=-4 - 3a_{n-1}\).
A program első argumentuma \(\displaystyle N\) értéke és a második egy kimeneti fájl legyen. A kimeneti fájlban soronként jelenítsük meg a sorozatok szóközzel elválasztott elemeit. (A fájlba íráskor se használjunk ciklust.)
Beküldendő a program forráskódja (i259.pas, i259.cpp, ...), valamint a program rövid dokumentációja (i259.txt, i259.pdf, ...), amely tartalmazza a megoldás rövid leírását, és megadja, hogy a forrásállomány melyik fejlesztő környezetben fordítható.
(10 pont)
I. 260. Készítsük el egy ,,Készpénzutalási megbízás'' másolatát a táblázatkezelő rendszerben! A nyomtatványon fehér hátterű az a rész, ahova a befizető írja az adatait, a csekk többi része sárga hátterű. A Feladóvevény fehér oszloppal van elválasztva a többi résztől. Az útmutató feliratok és keretezések pirosak. A befizető feketével írhassa az adatait. (A minta színesben is látható a hátsó belső borítón.)
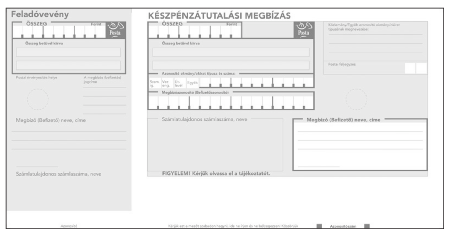
A Megbízó (Befizető) neve, címe címke alatti fehér területre írva az adatok a Feladóvevény sárga területén is jelenjenek meg.
A befizetendő összeget a Feladóvevény Összeg celláiba számjeggyel írhassuk be és ez a másik rész Összeg címkéje alatt is jelenjen meg.
Oldjuk meg, hogy a számjegyek szabályos beírása esetén az Összeg betűvel kiírva részben szövegesen jelenjen meg a befizetendő összeg. A számok tagolása a magyar helyesírás szabályainak feleljen meg. A megoldáshoz makró és segédcellák használhatók, amelyek a csekk megjelenítésén kívül jól láthatók legyenek.
Értékelés: legföljebb 5 pont szerezhető a számok helyes betűvel írásával és még 5 pont szerezhető a grafika minél pontosabb megvalósításával, ha az átalakítás működik.
Beküldendő a táblázatkezelő munkafüzet (i260.xls, i260.ods, ...), illetve egy rövid dokumentáció (i260.txt, i260.pdf, ...), amelyben szerepel a megoldáskor alkalmazott táblázatkezelő neve, verziószáma, valamint a megoldás rövid leírása.
(10 pont)
I. 261. Letölthető állományok a megoldáshoz: forras.txt, 1.jpg, 2.jpg, 3.jpg, 4.jpg
A gyufarejtvények bemutatására készítsünk ábrákat és négy weblapot. A weboldalak készítéséhez forrásként a forras.txt, az 1.jpg, a 2.jpg, a 3.jpg és a 4.jpg állományokat, illetve a megadott mintát használjuk fel. A honlapunkról letölthető a forras.zip állomány, amely a forrásállományokat tartalmazza tömörítve.
1. Képszerkesztő program segítségével készítsünk a honlap díszítéséhez csik.jpg néven egy képet az 1.jpg, a 2.jpg, a 3.jpg és a 4.jpg állományok képeinek egymáshoz illesztésével a minta szerint.
2. Rajzolóprogram segítségével készítsük el az abra1.png állományt a minta, valamint a rejt1.html oldalon látható gyufaszálakból álló ábra szerint.
3. Hozzunk létre négy weblapot rejtbev.html, rejt1.html, rejt2.html és rejt3.html néven. Mind a négy oldal következő tulajdonságai egyezzenek meg:
\(\displaystyle a\). A böngésző címsorában megjelenő cím legyen ,,Gyufarejtvény''.
\(\displaystyle b\). Az oldal háttérszíne legyen türkiz (#53868B kódú szín), a szöveg színe és a linkek minden állapotának színe fekete.
\(\displaystyle c\). Készítsünk egy \(\displaystyle 2\times 2\)-es táblázatot: A táblázat legyen középre igazított, 800 pont széles. A háttérszíne legyen fehér. Állítsunk be 2 pontos keretet és 10 pontos cellamargót.
\(\displaystyle d\). A táblázat első sorában vonjuk össze a cellákat és ide illesszük be a csik.jpg képet.
\(\displaystyle e\). A második sor első cellájának szélességét állítsa 150 pontosra. A cellába írjuk be a ,,Bevezető'', ,,1. rejtvény'', ,,2. rejtvény'' és ,,3. rejtvény'' szöveget. A szövegeket alakítsa linkké. A lapokon mindig három link van (az a szöveg nem hivatkozás, amely az aktuális oldalra mutatna). A linkeket igazítsa a mintának megfelelően.
4. A rejtbev.html lapon az elkészített egységes táblázat második sor, második cellájába illesszük be a forras.txt állományból a szöveget. A mintának megfelelően alakítsuk ki a bekezdéseket.
5. A ,,Gyufarejtvény'' szöveget formázzuk Címsor1-es stílussal és helyezzük középre.
6. Állítsunk be felsorolást a szabályokat leíró bekezdésekre és a minta alapján formázzuk félkövér stílussal a szabály leírás címét.
7. A rejt1.html oldalon az elkészített egységes táblázat második sorának második cellájában szúrjuk be az abra1.png képet és a hozzátartozó szöveget a forras.txt állományból illesszük be.
8. A további két rejtvényt nem adjuk meg. Keressünk tetszőleges másik két gyufarejtvényt és a hozzátartozó ábrákat abra2.png és abra3.png néven készítsük el.
9. Az általunk választott két gyufarejtvény alapján készítsük el a rejt2.html és a rejt3.html oldalakat és formázzuk a rejt1.html oldallal megegyező módon.
Minta: rejtbev.html

rejt1.html
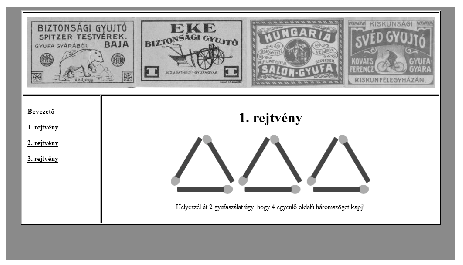
(A minták színesben is láthatók a hátsó belső borítón.)
Beküldendő egy tömörített állományban (i261.zip, i261.rar ...) a megoldáshoz szükséges összes állomány, illetve egy rövid dokumentáció (i261.txt, i261.pdf ...), amelyben szerepel a megoldáskor alkalmazott képszerkesztő, rajzoló és honlapszerkesztő program neve.
(10 pont)
 |
S-jelű feladatokA beküldési határidő 2011. március 10-én LEJÁRT. |
S. 60. Egy négyzet alakú földdarabból egy adott méretű, szintén négyzet alakú területet szeretnénk elkeríteni. A kerítéseknek párhuzamosaknak kell lenniük a földdarab oldalaival. Arra törekszünk, hogy minél több fa legyen az elkerített részben (a kerítés vonalára eső fákat úgy számoljuk, hogy belül vannak).
Írjunk programot, ami a standard bemenetről beolvassa a földdarab és az elkerítendő terület méretét, valamint a fák elhelyezkedését, és standard kimeneten megadja a kerítés egy optimális elhelyezését.
A bemenet szerkezete a következő: az első sorban három szóközzel elválasztott szám, a földdarab oldalhossza (\(\displaystyle 1 \le N \le 4000\)), az elkerítendő terület oldalhossza (\(\displaystyle 1 \le M \le N\)) és a fák száma (\(\displaystyle 1 \le K \le 1\;000\;000\)) található. A következő \(\displaystyle K\) sor mindegyikében szóközzel elválasztva egy-egy fa sor- és oszlopkoordinátái szerepelnek (\(\displaystyle 0 \le I, J \le N\)). Minden koordináta egész szám, és nincs két olyan fa, amelyeknek mindkét koordinátája megegyezik.
A standard kimenet első sorába írjuk ki az elkerített részbe kerülő fák számát, a második sorába pedig az elkerített négyzet bal felső sarkának sor- és oszlopkoordinátáit szóközzel elválasztva. Több megoldás esetén bármelyik megadható.
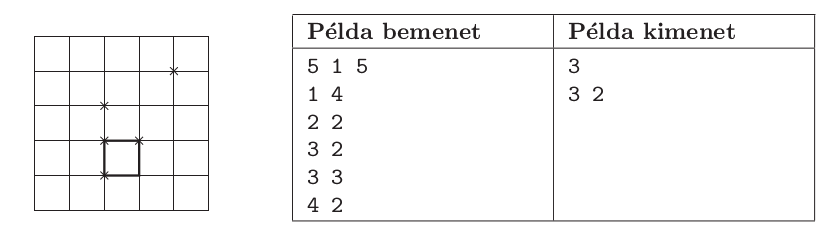
A futási időlimit tesztesetenként 10 másodperc.
Beküldendő a feladat megoldását tartalmazó forrás és projektállományok (az .exe és más a fordító által generált kiegészítő állományok nélkül), valamint a megoldás menetét röviden bemutató dokumentáció egy tömörített mappában.
(10 pont)
Figyelem!
Az informatika feladatok megoldásait ne e-mailben küldd be! A megoldásokat az Elektronikus munkafüzetben töltheted fel.

