KöMaL Problems in Mathematics, October 2011
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on November 10, 2011. |
K. 301. A box contains red and yellow balls. If one red ball were removed, one-seventh of the remaining balls would be red. If 5 yellow balls were removed instead, one-sixth of the remaining ones would be red. How many balls are there in the box?
(6 pont)
solution (in Hungarian), statistics
K. 302. Find all natural numbers, such that the third and fourth powers of the number together contain each digit exactly once.
(6 pont)
solution (in Hungarian), statistics
K. 303. How many triangles, rhombuses and cyclic trapeziums are there in the diagram?
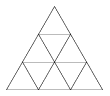
(6 pont)
solution (in Hungarian), statistics
K. 304. Points X and Y divide the sides AB and CD, respectively, of a rectangle ABCD in a 1:2 ratio, as shown in the figure. What is the ratio of the areas of the grey quadrilateral and the rectangle ABCD?
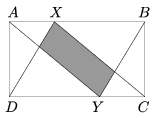
(6 pont)
solution (in Hungarian), statistics
K. 305. Satellite pictures of some dry regions of the United States show interesting circular features. (E.g. to view the area of ZIP code 79068 in Texas, enter TX 79068 for search in Google Earth.) The circles are formed owing to an irrigation technology involving a long rod revolving about its midpoint or an endpoint. Since the water does not reach the entire area of the field, only the interior of the circles, part of the field will not have plants growing on it. Three brothers, Joe, Jim and Jack each have a square field 1 km on a side. The irrigated areas on their fields are laid out as shown in the figure. In Jack's arrangement, the radius of the smaller circles is 210.5 m. Which of the brothers has the most productive arrangement of circles on his field, that is, which of them can use the greatest fraction of his field for growing plants?
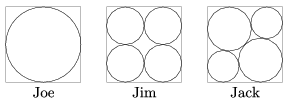
(6 pont)
solution (in Hungarian), statistics
K. 306. A 4×4-es square table is filled in with the digits of 2011, so that each row, column and diagonal contains 2, 0, 1, 1 in some order. In how many different ways is that possible?
(6 pont)
 |
Problems with sign 'C'Deadline expired on November 10, 2011. |
C. 1090. The solid in the picture is glued together out of thirteen regular dice. What is the maximum possible number of dots on its surface?
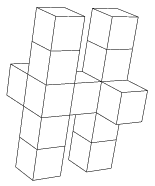
(5 pont)
solution (in Hungarian), statistics
C. 1091. In the lottery, 5 numbers are drawn out of the numbers 1 to 90. One time, the following numbers were drawn, listed in increasing order: ,
,
,
,
. The sum of the five numbers is
, the product of the third and second numbers is
, and the product of the third and fifth numbers is
. Determine the digits a, b, c, d, e.
(5 pont)
solution (in Hungarian), statistics
C. 1092. C is an interior point of the line segment AB. Regular triangles are drawn over the line segments AC and BC on one side of AB, and a regular triangle is drawn over the whole AB on the other side. Prove that the centroids of the three triangles form a regular triangle.
(5 pont)
solution (in Hungarian), statistics
C. 1093. The value of the function f(x) for a real number x is the smallest value out of x2-4x+3, x-1 and -x+7. Determine the number of solutions of the equation f(x)=c, depending on the real parameter c.
(5 pont)
solution (in Hungarian), statistics
C. 1094. In an isosceles right-angled triangle ABC, H is the point closer to C that divides the leg BC in a 3:1 ratio. G is the point on leg CA such that CG:GA=3:2. Find the measure of the angle enclosed by the line segments HA and GB.
(5 pont)
 |
Problems with sign 'B'Deadline expired on November 10, 2011. |
B. 4382. Let x be an integer. Prove that if is an integer then it is a square number.
(3 pont)
solution (in Hungarian), statistics
B. 4383. ABCD is a convex quadrilateral, such that AB>BC>CD>DA. The inscribed circles of the triangles ABD and BCD touch the diagonal BD of the quadrilateral at the points E and F, respectively. Show that EF=GH.
(Suggested by Sz. Miklós, Herceghalom)
(3 pont)
solution (in Hungarian), statistics
B. 4384. According to problem B. 4283. of this journal, if a 23×23 square is dissected into 1×1, 2×2 and 3×3 squares then at least one of the pieces must be a 1×1 square. Given that there is exactly one 1×1 piece, find its possible positions in the big square.
(Suggested by Z. Gyenes, Budapest)
(5 pont)
solution (in Hungarian), statistics
B. 4385. Solve the simultaneous equations {x}={x2}={x3} (where {y} denotes the fractional part of the number y, obtained by subtracting from y the greatest integer not greater than y).
(4 pont)
solution (in Hungarian), statistics
B. 4386. Is there a rational number such that by cancelling some digits out of its decimal form, the digits of 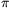 are left?
are left?
(4 pont)
solution (in Hungarian), statistics
B. 4387. In the cyclic hexagon ABCDEF, AB=BC, CD=DE and EF=FA. Prove that the area of the triangle BDF is half the area of the hexagon.
(4 pont)
solution (in Hungarian), statistics
B. 4388. D is an interior point of side AB of an acute-angled triangle ABC. The line drawn through D parallel to side AC intersects side BC at E, and the line drawn through D parallel to side BC intersects side AC at F. The other intersection of the circles ADF and BDE is G. Prove that ABEF is a cyclic quadrilateral if and only if G lies on the line segment CD.
(Suggested by Sz. Miklós, Herceghalom)
(4 pont)
solution (in Hungarian), statistics
B. 4389. Given four points A, B, C and D on a line in this order, consider all pairs of touching circles such that one circle passes through A and B and the other passes through C and D. Determine the locus of the points of contact.
(4 pont)
solution (in Hungarian), statistics
B. 4390. How many solutions does the equation have in the interval [0,20]?
(4 pont)
solution (in Hungarian), statistics
B. 4391. A height of a pentagon is defined as the distance of a vertex from the opposite side. Let P be a pentagon with all angles equal to 108o and all heights different. Show that it is possible to number the consecutive vertices of P in an appropriate direction around the pentagon, such that the corresponding heights satisfy the inequalities h1>h3>h4>h5>h2.
(Suggested by P. Kevei and V. Vígh, Szeged)
(5 pont)
 |
Problems with sign 'A'Deadline expired on November 10, 2011. |
A. 542. We have 1000 coins, but 100 of them are counterfeit. We know the weight of the real coins and it is known that the counterfeit coins are lighter than the real coins, but they may have different weights. Using a scale we want to find a counterfeit coin. Every time we can measure the total weight of a subset of the coins; the result indicates whether that set contains a counterfeit coin or not. How many measures are needed to find a counterfeit coin for sure?
(Suggested by Dömötör Pálvölgyi, Budapest)
(5 pont)
A. 543. The sum of the probabilities of some (finitely many) independent events is 4. Prove that with probability higher than 1/2, the number of occurred events is congruent to 0 or 3 modulo 4.
(Suggested by Endre Csóka, Budapest)
(5 pont)
A. 544. A circle k with center O and four distinct fixed points A, B, C, D lying on it are given. The circle k' intersects k perpendicularly at A and B. Let X be a variable point on the line OA. Let U, other than A, be the second intersection of the circles ACX and k'. Let V, other than A, be the second intersection of the circles ADX and k'. Let W, other than B, be the second intersection of the circle BDU and the line OB. Finally, let E, other than B, be the second intersection of the circles BVW and k. Prove that the location of the point E is independent from the choice of the point X.
(5 pont)
Upload your solutions above.
