KöMaL Problems in Mathematics, January 2012
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on February 10, 2012. |
K. 319. a) What digits are denoted by a, and by b if is divisible by 3? b) What may c and d be if
is divisible by 4?
(6 pont)
solution (in Hungarian), statistics
K. 320. The four-digit number consists of four different positive digits, and
. How many such four-digit numbers
are there?
(6 pont)
solution (in Hungarian), statistics
K. 321. We cut a regular hexagon shaped tabletop into two parts along his symmetry diagonal, like this we got two symmetric trapezoid tabletops. In the reading area of a library, there are such trapezoidal tables in three colours: green, blue and red. We compiled a bigger regular hexagon from eight such tabletops.
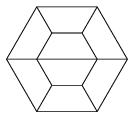
a) In how many different ways is it possible to make this arrangement if two tables of the same colour cannot have an edge in common? (Arrangements obtained from each other by rotation are not considered different.)
b) At the long side of a trapezoidal table there is room for two chairs, while at each of the other sides there is only room for one chair. Therefore, 12 people can be seated comfortably around this hexagonal arrangement of tables. How many tables are needed for a big hexagon around which 18 people can be comfortably seated?
(6 pont)
solution (in Hungarian), statistics
K. 322. k of the six-digit numbers of the form , and n of the six-digit numbers of the form
are divisible by 15. Calculate the ratio
.
(6 pont)
solution (in Hungarian), statistics
K. 323. The apex angle of the isosceles triangle ABC is 120o, and the midpoint of base AB is F. The angle bisector of  ACF intersects base AB at point H. a) Prove that AH=CH. b) Prove that AH is one-third of the line segment AB.
ACF intersects base AB at point H. a) Prove that AH=CH. b) Prove that AH is one-third of the line segment AB.
(6 pont)
solution (in Hungarian), statistics
K. 324. 3 bigger cubes are built out of 99 small red cubes. Then the faces of the big cubes are painted white. Finally, all three big cubes are taken apart again, and a small cube is selected at random. The selected small cube is rolled. What is the probability that it will have a red face on top?
(6 pont)
 |
Problems with sign 'C'Deadline expired on February 10, 2012. |
C. 1105. Two regular polygons are drawn. In one of them, sides are drawn in red and diagonals are drawn in green. In the other, sides are green and diagonals are red. There are 103 red line segments and 80 green line segments altogether. How many sides do the polygons have?
(5 pont)
solution (in Hungarian), statistics
C. 1106. Depending on the parameter a, how many zeros does the function defined by
have?
(5 pont)
solution (in Hungarian), statistics
C. 1107. Solve the following simultaneous equations on the set of real number pairs: 3x2-xy+3y2=16, 7x2-4xy+7y2=38.
(5 pont)
solution (in Hungarian), statistics
C. 1108. In a right-angled triangle ABC, the altitude drawn to the hypotenuse is CD. Prove that the sum of the areas of the circles inscribed in triangles ADC and BCD equals the area of the inscribed circle of triangle ABC.
(5 pont)
solution (in Hungarian), statistics
C. 1109. There were 14 multiple choice questions on a quiz, with 4 answers to each question. The best score was 10. What is the probability of achieving this score if the answers are selected at random?
(5 pont)
 |
Problems with sign 'B'Deadline expired on February 10, 2012. |
B. 4412. When the age of the ship is the same as the captain's age now, the captain will be exactly 32 years older than the ship was when the captain was half as old as the ship is now. How old is the captain?
(3 pont)
solution (in Hungarian), statistics
B. 4413. The area of a symmetrical trapezium is 4 units, it is not a rectangle, and it can be divided into four congruent trapezia that are similar to
. Determine the sides and angles of
.
(4 pont)
solution (in Hungarian), statistics
B. 4414. There are 98 sticks lying on the table, their lengths are 1,2,3,...,98 units. Ann and Bill play the following game: With Ann starting the game, they take turns removing one stick of their choice. The game ends when there remain exactly three sticks on the table. Ann wins if the three sticks can form a triangle. Otherwise, Bill wins. Which player has a winning strategy?
(4 pont)
solution (in Hungarian), statistics
B. 4415. Let B be an interior point of a line segment AC. The Thales circles of the line segments AB, BC and AC are k1, k2 and k3, respectively, with radii of r1, r2 and r3. A common exterior tangent of circles k1 and k2 cuts the circle k3 into two circular segments. The radius of the circle inscribed in the smaller circular segment is r4. Prove that r1.r2=r3.r4.
(Suggested by Sz. Miklós, Herceghalom)
(4 pont)
solution (in Hungarian), statistics
B. 4416. Given a vertex, the orthocentre and the centroid, construct the triangle.
(4 pont)
solution (in Hungarian), statistics
B. 4417. Solve the equation . (3 points)
(3 pont)
solution (in Hungarian), statistics
B. 4418. Regular triangles ABD, BCE and CAF are drawn over the sides of triangle ABC on the outside. Let G, H and I denote the midpoints of line segments DE, EF and FD, respectively. Prove that the sum of the angles AHB, BIC and CGA is 180o.
(Suggested by Sz. Miklós, Herceghalom)
(5 pont)
solution (in Hungarian), statistics
B. 4419. Jack Potter is an addicted gambler. Yesterday, he threw 20 000 forints (HUF, Hungarian currency) in a one-armed bandit machine without his family knowing about it. To make things worse, he took that money from the amount that the family reserved for food. To avoid the affair being revealed, today he is taking the remaining 40 000 forints of the family, too, and goes back to the casino to play roulette. Since he does not want to risk too much, he is betting 1000 forints on red or on black in each game. If he wins, which has a probability of 18/37, then he gets another 1000 forints. Otherwise he loses his bet. He stops playing either when he has gathered a total of 60 000 forints -- in that case he can put all the money back in its place -- or when he has lost all the money. What is the probability that Jack Potter will manage to gather the 60 000 forints?
(Based on the idea of D. Pálvölgyi, Budapest)
(5 pont)
solution (in Hungarian), statistics
B. 4420. The lengths of the edges of a cuboid are 7, 14 and 21 units. Which pair of skew face diagonals lying on adjacent faces have the smallest distance?
(Based on a Kavics Kupa problem, 2011)
(4 pont)
solution (in Hungarian), statistics
B. 4421. Let t denote a fixed integer. Show that for every odd prime number p, there exists a positive integer n, such that (3-7t)2n+(18t-9)3n+(6-10t)4n is divisible by p.
(Suggested by K. Kalina, Budapest)
(5 pont)
 |
Problems with sign 'A'Deadline expired on February 10, 2012. |
A. 551. Show that there exist infinitely many pairs (a,b) of positive integers with the property that a+b divides ab+1, a-b divides ab-1, b>1 and .
(5 pont)
A. 552. Prove that for an arbitrary sequence of nonnegative real numbers and
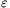 >0 there exist infinitely many positive integers n for which
>0 there exist infinitely many positive integers n for which .
(Schweitzer-competition, 2011)
(5 pont)
A. 553. Suppose that in a simple graph G with n vertices the minimal degree 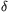 (G) is at least 3n/4. Prove that for any 2-coloring of the edges of G, there is a connected subgraph with at least
(G) is at least 3n/4. Prove that for any 2-coloring of the edges of G, there is a connected subgraph with at least 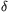 (G)+1 vertices whose edges have the same color.
(G)+1 vertices whose edges have the same color.
(Schweitzer-competition, 2011)
(5 pont)
Upload your solutions above.
